Регрессионный анализ данных. Решение задач прогнозирования экономических процессов

Компьютерные технологии
(Аспирантура)

Практическое занятие 3

Тема: Регрессионный анализ данных. Решение задач прогнозирования экономических процессов.

Цель – освоить методику поиска корней уравнений, определения закономерностей (тренда) протекания экономических процессов, решения задач экстраполяции и интерполяции.

Время – 2 часа

Порядок выполнения работы:

Задание 1.

1.  В соответствии с вариантом найти корни уравнения. Для этого:

·  создать таблицу с исходными данными задачи;

·  построить график функции f(x) = 0;

·  локализовать корни (с использованием графика оценить приближенное значение корней);

·  найти все корни уравнения с точностью 10^-5.

Варианты заданий 1

№ варианта	Уравнение
1	x3  – 0,41x2 – 0,7004x + 0,139104 = 0
2	x3  – 2,29x2 + 1,4355x - 0,20886 = 0
3	ln(x+3) – x3 + x2 + x – 1,5 = 0
4	x3  + 2,84x2 – 5,6064x - 6,766336 = 0
5	x3  + 0,85x2 – 0,4317x - 0,24391 = 0
6	x3  + 1,41x2 – 5,4724x – 7,380384 = 0
7	x3  + 0,77x2 – 0,2513x + 0,016995 = 0
8	x/( x3 – x + 1) –0,37 = 0
9	x3  + 0,77x2 – 0,2513x + 0,016995 = 0
10	x3  + 0,88x2 – 0,3999x + 0,037638 = 0
11	x3 – ln(x+4) – x2 – x + 2 = 0
12	x3  – 2,31x2 + 2,7843x + 0,643787 = 0
13	x3  – 0,12x2 – 1,4775x + 0,191906 = 0
14	x3  + 0,78x2 – 0,8268x + 0,146718 = 0
15	x3  – 2,56x2 – 1,3251x + 1,395006 = 0

№ вар	Функция спроса D(Q)	Функция предложения S(Q)	Qнач	Qкон	DQ
1	30; 28; 27; 20; 15; 13; 8; 5	(Q + 3)×arctgQ	1	8	1
2	10 – Q + 50/Q	4; 7; 12; 15; 21; 24; 26; 31; 33; 35	2	11	1
3	36; 32; 28; 25; 24; 21; 17; 15; 14	0,5×(Q2 + Q + 1)	1	9	1
4	37; 32; 28; 25; 24; 22; 17; 15	Q×lnQ + 10	3	10	1
5	25 – ((Q/10)3 + Q2/2 + Q)	3, 7, 11, 14, 16, 19, 18, 18, 20, 21	1	5,5	0,5
6	15; 12; 11; 9; 7; 5; 4; 3; 1	20 – (30×arctgQ2)/Q	2	10	1
7	25×Q3×exp(-Q)	6; 8; 11; 15; 22; 25; 29; 32; 34	3	11	1
8	14; 12; 10; 7; 4; 2; 2; 1	9 × (1 – cos(Q/4))	2	9	1
9	25 – 5×lnQ× arctgQ	2, 3, 3, 5, 8, 12, 17, 20, 26	2	18	2
10	37; 32; 28; 26; 24; 21; 17; 15	10 + Q2× ln(0,5×Q)	2	5,5	0,5
11	40 – Q2 + 5×Q	5; 7; 10; 15; 23; 26; 29; 38	2	9	1
12	24; 20; 18; 17; 14; 11; 7; 2	0,3×Q3 + 3	1	4,5	0,5
13	10 × (1 + cos(Q/4))	1; 2; 4; 7; 9; 10; 13; 17; 20; 22	1	10	1
14	12; 10; 9; 8; 7; 5; 4; 1	0,6×e0,2×Q	1	15	2
15	Q3/exp(Q – 3)	3; 4; 8; 12; 15; 14; 20; 22; 30	3	11	1

Варианты заданий 2

Задание 2

Кривые спроса D(Q) и предложения S(Q) на рынке товаров заданы в виде экспериментальных данных или аппроксимируются некоторыми функциями (таблица).

Составить таблицу с исходными данными.

Построить графики функций. Добавить линии тренда для экспериментальных данных, получить уравнение тренда. Подбор осуществить по критерию максимума R². Используя возможности Excel, найти равновесную точку E спроса и предложения товара на рынке.

Контрольные вопросы

1.  Охарактеризуйте общую задачу поиска корней уравнения.

2.  Что такое локализация корней уравнения?

3.  Как установить требуемую точность нахождения корней уравнения?

4.  Найти корни уравнения y(x) = f(x) – 0,5, где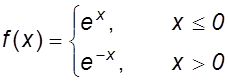

(x изменяется от –3 до 3 с шагом 1).

5.  Что такое тренд, какие параметры тренда можно установить на диаграмме?