Некоторые проблемы построения экспертных рейтингов финансовых рынков, страница 2

Желание уменьшить относительность порядковых шкал, придать им хотя бы внешнюю независимость от измеряемых величин побуждают исследователей к различным модификациям, придающим порядковым шкалам некоторое усиление. Однако произвольное приписывание баллов предварительно проранжированным альтернативам, как это делается в методике Д.А.Р., абсолютно недопустимо, так как получаемые результаты после такого "усиления" порядковой шкалы не имеют смысла. Более того, в некоторых учебниках по количественному экономическому анализу  (например, Баканов М.И., Шеремет А.Д. — "Теория экономического анализа") предлагается проранжированные места объектов (ранги) складывать с определенными "весами" для получения общего ранжирования!

Что же делать в тех случаях, когда экспертная информация представляется в порядковой шкале? Может быть несколько подходов к обработке экспертной информации в порядковых шкалах. В первом случае можно использовать результаты теории выбора – процедуры с вспомогательной шкалой (процедуру Борда, плюралитарную процедуру, процедуру Янга, процедуру Кемени), а также процедуры, использующие в качестве вспомогательной структуры мажоритарный граф (правило Кондорсе, парно-доминантное правило выбора, правило фон Неймана-Моргенштерна, правило Коупленда, правило Фишберна, правило Ричелсона, правила турнирных матриц и т.д.). Наиболее простой является процедура Борда, которая представляется следующим образом. Результаты опроса N экспертов сводятся в таблицу. В i-й строке стоят места (ранги), данные i-м экспертом ранжируемым объектам. В (N+1)–й строке стоят суммы рангов, полученных объектами от экспертов. Все n объектов упорядочиваются в соответствии с величиной k_s, определяемой по форму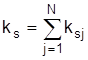ле . На первое место ставится объект, у которого k_s минимально и т.д. Степень согласованности мнений экспертов определяется при помощи коэффициента конкордации W. Более обоснованной, хотя и более сложной, является процедура нахождения медианы Кемени, которая вычисляется по формуле 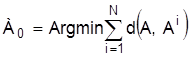, где d — некоторый аналог "расстояния" между ранжировками по отношению к А_o. Недостатком указанных подходов является отсутствие сведений об истинном расстоянии между альтернативами (предпочтениями экспертов).

Второй подход позволяет получить хотя бы очень грубую информацию о силе предпочтения экспертов с помощью порядковой шкалы Черчмена-Акоффа. Использование этой шкалы при достаточно сильных требованиях к весовым коэффициентам измерения позволяет перевести порядковую шкалу в разряд более сильных шкал. Сначала эксперты упорядочивают объекты в порядке предпочтения. Затем их просят поставить в соответствие (приписать) альтернативам любые числа между 0 и 1, выразив грубо "силу" предпочтения. Целью является уточнение с помощью дальнейших вопросов действительной силы предпочтений экспертов.

Недостатком этого метода является то, что предположение об аддитивности весов предпочтения экспертов может иногда не выполняться.

Еще одним подходом может быть использование вербальных шкал, по своей сути являющихся порядковыми. Шкалы интенсивностей критериальных свойств, выраженные в словах, называются вербальными, или лингвистическими. Неравномерность вербальных шкал, различие в понимании их значений экспертами общеизвестны. Поэтому представляется рациональным построить равномерную универсальную шкалу интенсивности критериальных свойств. Крайними точками этой шкалы будут минимальная l_min и максимальная l_max интенсивности критериальных свойств. Укороченный вариант этой шкалы (из пяти оценок) используется при анализе покупательского спроса. Статистически были установлены числовые интервалы ( () для этих оценок – шкала Харрингтона: 1) очень высокая интенсивность критериального свойства ( (=1.0-0.8); 2) высокая ( (=0.8-0.63); 3) средняя ( (=0.63-0.37); 4) низкая ( (=0.37-0.2); 5) очень низкая ( (=0.2-0.00). В Украине имеется пример использования шкалы Харрингтона для ранжирования банков (методика А. Гуревича).

Таким образом, в докладе на понятийном уровне была показана некорректность экспертной методики рейтингования субъектов фондового рынка Украины и предложены некоторые общие возможные подходы к ее улучшению. В заключение хотелось бы предостеречь исследователей от слишком вольного обращения с цифрами, потому что в погоне за "экономическим" смыслом выводимых формул может потеряться их математический смысл.