Використання економіко-математичного моделювання в процесі дослідження організації мотивації праці на підприємствах

досліджуваний елемент, то вони мають однакову значущість, отже при порівнянні їм ставиться 1 бал (наприклад, фондовіддача і продуктивність праці мають приблизно однаковий вплив на матеріально-організаційний елемент мотивації праці, а використання робочого часу і відсоток працівників, що пройшли підвищення кваліфікації - на соціально-економічний елемент мотивації праці та ін.).

За умови існування певних переваг у значущості одного фактора над іншим (наприклад, при оцінці впливу матеріально-організаційного і соціально-економічної елементу на мотивацію праці перший явно переважає) проставляється  3 бали.

Якщо вплив одного фактора істотно переважає дію іншого, як, наприклад, при порівнянні впливу на фондовіддачу фактору організації виробництва і рівня заробітної плати, тоді виставляється оцінка 5 балів.

Якщо при оцінці впливу факторів значущість одного є очевидною чи абсолютною, тоді проставляється, відповідно, 7 чи 9 балів.

Правомочність цієї шкали доведена теоретично при порівнянні з багатьма іншими шкалами [12].

Ранжування елементів, що аналізуються з використанням матриці парних порівнянь [Е], здійснюється на основі головних власних векторів, що отримують в результаті обробки матриць.

Обчислення головного власного вектору W позитивної квадратної матриці  [Е] проводиться на основі тотожності:

ЕW = W,                                                                                                                      (1.1)

де  - максимальне власне значення матриці [Е].

Для позитивної квадратної матриці [Е] правий власний вектор W, що відповідає максимальному власному значенню , з точністю до постійного співмножника С можна розрахувати за формулою:

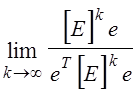 = СW,                                                                                                                      (1.2)

де е = - одиничний вектор;

k = 1, 2, 3, ... - показник ступіні;

С - константа;

Т - знак транспонування.

Обчислення власного вектору W за формулою (1.2) проводяться до досягнення завданої точності:

,                                                                                                                      (1.3)

де  l - номер ітерації, такої, що l = 1 відповідає k = 1; l = 2,  k =2; l = 3,  k = 3 і т.д.; 

ξ - допустима погрішність.

Із достатньою для практики точністю можна прийняти  ξ = 0,01 незалежно від порядку матриці.

Максимальне власне значення обчислюється за формулою:

 = [Е] W                                                                                                                      (1.4)

Після побудови матриць парних порівнянь проводиться оцінка однорідності суджень. Вона має дуже велике значення, бо при вирішенні практичних задач через неможливість вираження людських відчуттів точною математичною формулою відбувається порушення кількісної та транзитивної однорідності. При порушенні однорідності ранг матриці буде відрізнятися від одиниці і вона матиме декілька власних значень. Однак при незначних відхиленнях суджень від однорідності одне з власних значень буде значно більше інших і приблизно дорівнюватиме порядку матриці. Таким чином, для оцінки однорідності суджень експерта необхідно використовувати відхилення величини максимального власного значення  від порядку матриці n. Однорідність суджень оцінюється індексом однорідності (ІО) чи відношенням однорідності (ВО) відповідно до таких виразів:

ІО = ( – n) / (n – 1),                                                                                                                      (1.5)

ВО = ІО / М(ІО),                                                                                                                          (1.6)

де М(ІО) - середнє значення (математичне очікування) індексу однорідності випадковим чином складеної матриці парних порівнянь [Е], що ґрунтується на експериментальних даних [12].

В якості припустимого використовується значення ВО  0,10. Якщо для матриці парних порівнянь відношення однорідності ВО > 0,10, то це свідчить про суттєве порушення логічності суджень, припущене