Фильтрация данных на основе быстрого преобразования Фурье

Фильтрация данных на основе быстрого преобразования Фурье (БПФ)

Описание рабочих массивов:

> restart;

> with(stats): with(plots):

> N := 64:

> F := array(1 .. N):

> R := array (1 .. N) :

> Y := array(1 .. N):

> Z := array(1 .. N):

> ZY := array(1 .. N):

> Y1 := array(1 .. N):

> Z1 := array(1 .. N):

> Vx := array ( 1 .. N) :

Определение исходного сигнала и функции шума

random - функция, генерирующая шум с равномерным распределением,  fon-- параметр шума.

Исходную функцию занесем в массив F, а зашумлённую - в массивы Y (действительная часть) и Z(мнимая часть). Массивы Y1 (действительная часть) и Z1 (мнимая часть) будем использовать для хранения модифицируемого спектра сигнала.

Обращаем внимание: 2^6 = 64 ! Т.е. размер массивов должен быть кратен целочисленной степени двойки!

Элементы массива Z присваиваем равными нулю, т.к. в нашем сигнале только действительная составляющая.

Создадим собственную пользовательскую функцию U(t) = sin (t) и построим её график в пределах от  Tb до Te  :

> U := (t) -> sin (100*2*Pi*t) :

> Tb := 0: Te := 0.01:

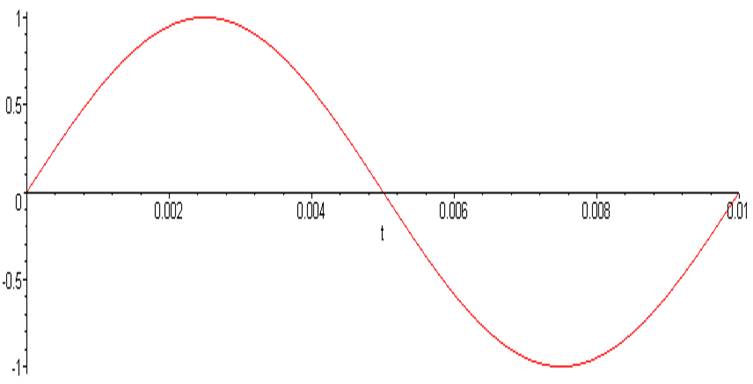
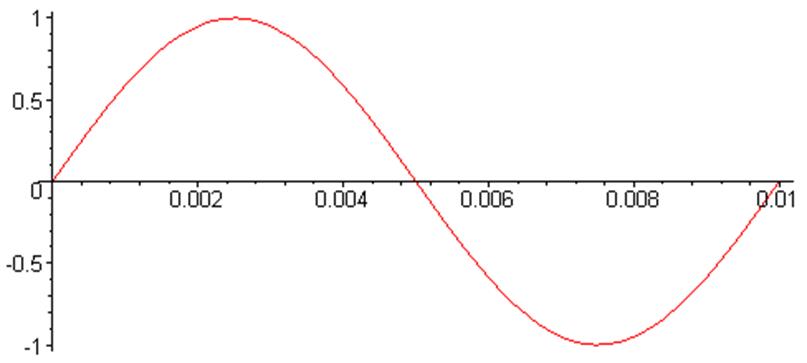
График исходной функции:

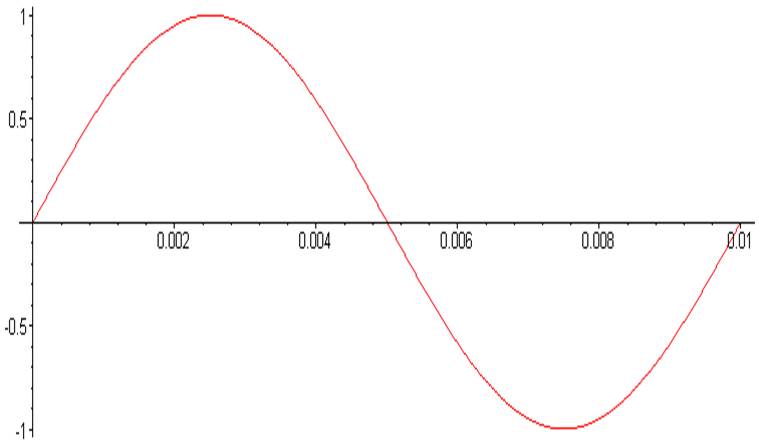
> plot ( U (t) , t = Tb .. Te) ;

Запишем в массив F ординаты функции, а в массив Vx - её абсциссы.

> delta := (Te - Tb) / ( N - 1 ) :

> Vx [1] := Tb:

> for i  from 2 by 1 to N do Vx[ i ] := evalf ( Vx [ i - 1 ] + delta ) od :

> for i  from 1 by 1 to N do  F [i] := U ( Vx [i] )  end do:

Построим графики изменения значений массивов F и  Vx,  как функций от номера индекса массива:

> plot ( [ F[n] , Vx[n] ] , n = 1 .. 64 ) ;

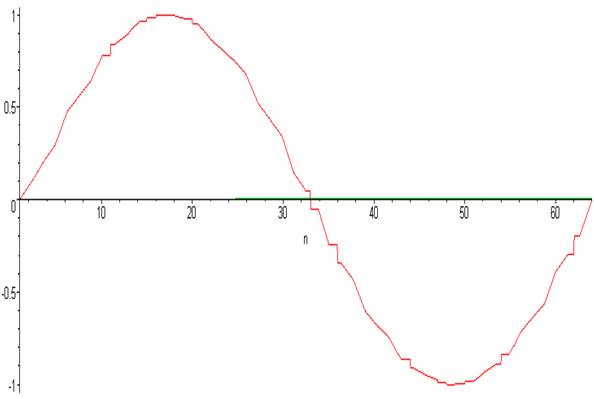
Ниже построен график зависимости, абсциссы и ординаты которой мы записали в массивы, как параметрической кривой, зависящей от индекса массивов.

Нетрудно убедиться, что график совпадает с исходной функцией.

> Sgr := plot ( [ Vx[n] , F[n]  , n = 1 .. N ] ) :

> Sgr;

> fon:=.3:

> for i from 1 to N do  R[i] := fon*(stats[random, uniform](1)-1/2): Y[i]:= evalf ((F[i] + R[i])):  ZY[i]:=0 od:

> print(Y,Z):

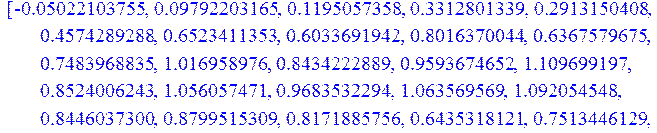
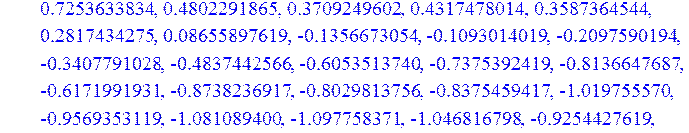
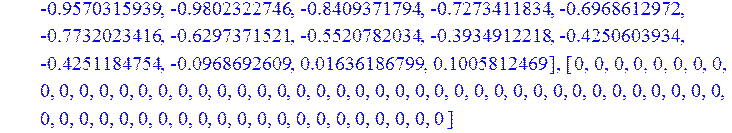
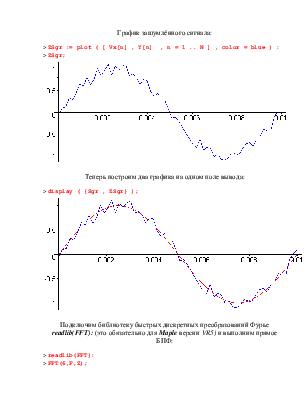
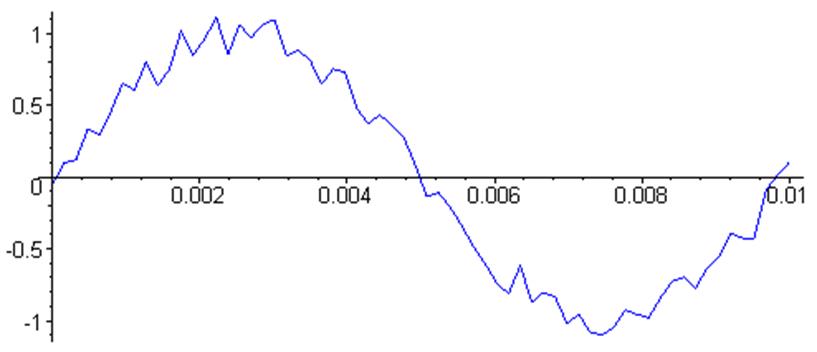
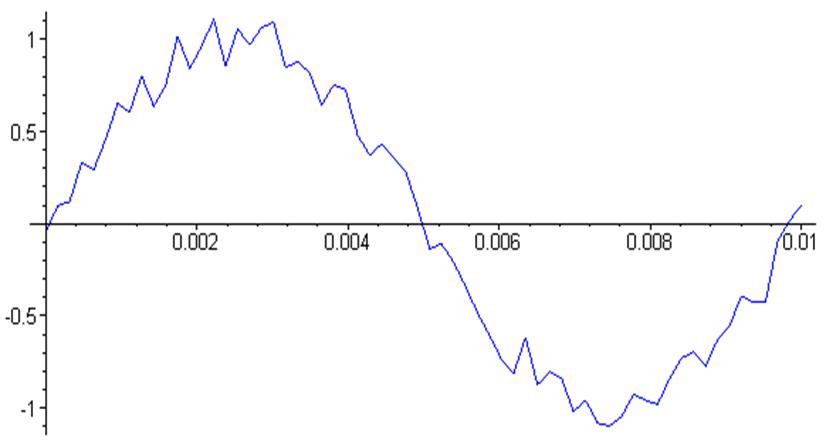
График зашумлённого сигнала:

> ZSgr := plot ( [ Vx[n] , Y[n]  , n = 1 .. N ] , color = blue ) :

> ZSgr;

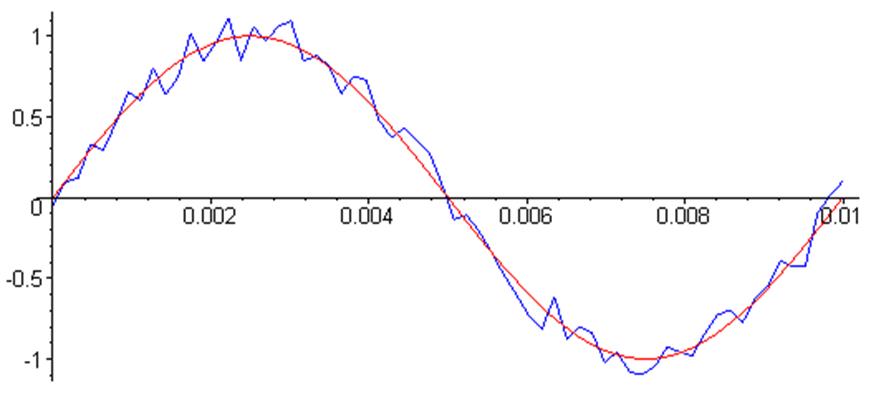
Теперь построим два графика на одном поле вывода:

> display ( {Sgr , ZSgr} );

Подключим библиотеку быстрых дискретных преобразований Фурье readlib(FFT): (это обязательно для Maple версии VR5) и выполним прямое БПФ:

> readlib(FFT):

> FFT(6,F,Z);

> FFT(6,Y,ZY);

>  #for i from 1 to Nmax do print (evalf (F[i]) ) od:

> #print (Z) :

> #for i from 1 to Nmax do  print (evalf (abs(F[i] + I*Z[i])) ) od ;

Следует иметь ввиду, что после выполнения БПФ в массивахYиZхранится уже не исходная функция, а спектр сигнала -Y (действительная часть) и Z(мнимая часть). В силу этого, если есть необходимость хранить исходную функцию, то для этого потребуется определить дополнительно два массива, в которые предварительно надо записать координаты исходной функции.

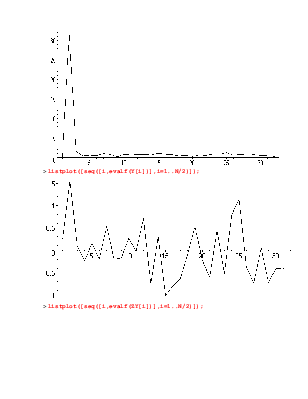
Построим графики модулей дискретного спектра исходного и зашумлённого сигналов, а также действительной и мнимой частей дискретного спектра зашумлённого сигнала:

> listplot([seq([i,evalf(abs(F[i] + I*Z[i]))],i=1..N/2)]);

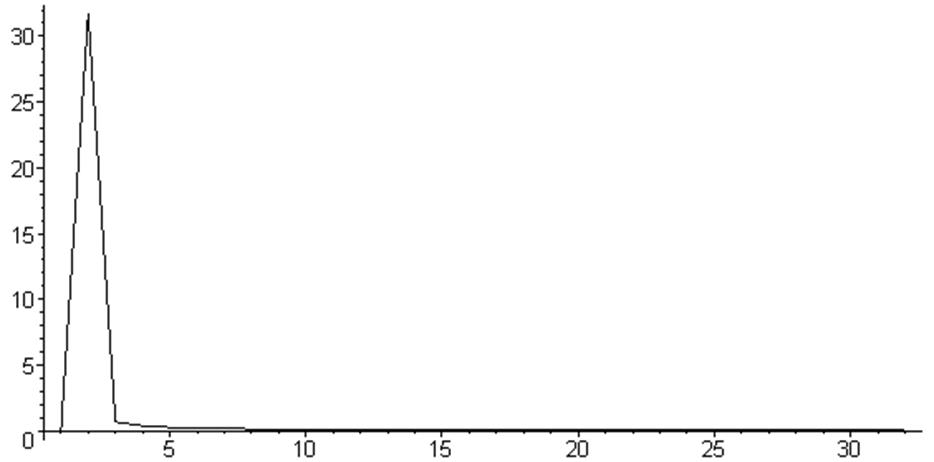
> listplot([seq([i,evalf(abs(Y[i] + I*ZY[i]))],i=1..N/2)]);

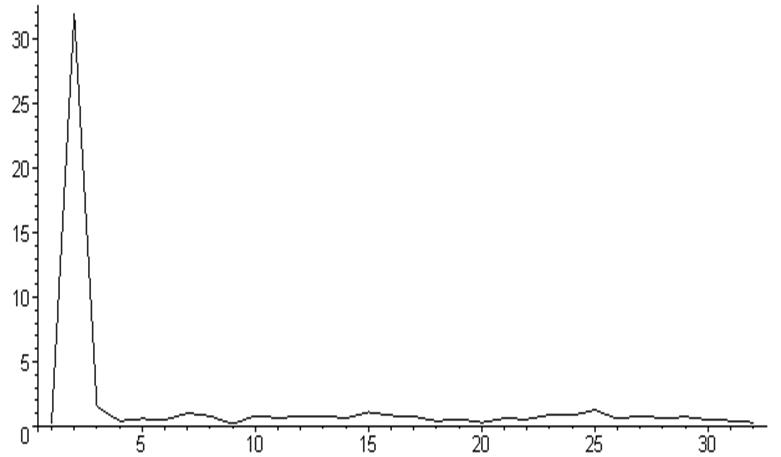
> listplot([seq([i,evalf(Y[i])],i=1..N/2)]);

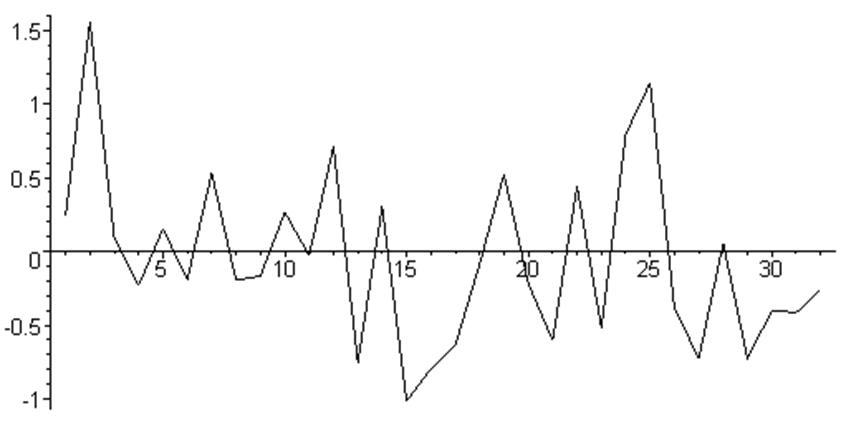
> listplot([seq([i,evalf(ZY[i])],i=1..N/2)]);

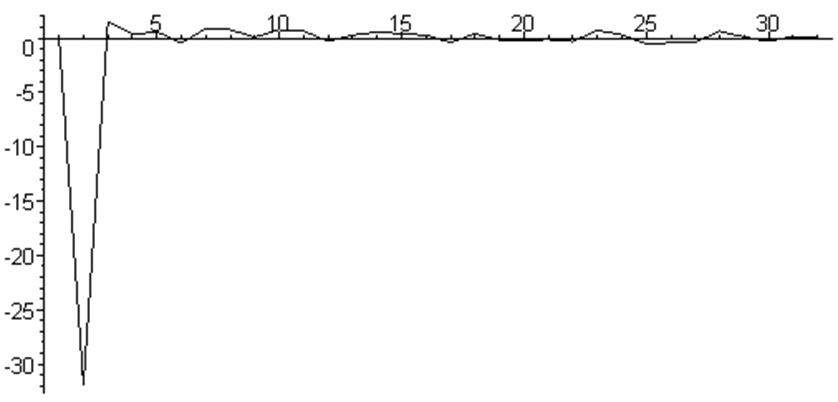
Фильтрация сигнала

Предварительно зададим аналитическую функцию  filtr(x),  при помощи которой отфильтруем часть спектра зашумлённого сигнала,  и

построим её график.

 (При выполнении лабораторной работы необходимо самостоятельно подобрать подобную кривую. Это можно сделать, например, задав координаты требуемых точек, через которые затем следует провести интерполирующую или аппроксимирующую кривую. Далее посредством полученной функции необходимо изменять амплитуды гармоник спектра.)

> filtr:= unapply(.02/((x-2)^2+.01),x);

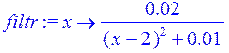
> plot(filtr(x),x=0..5);

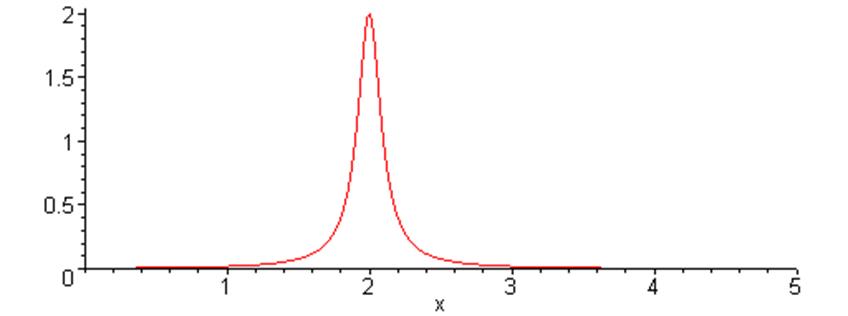
Выполним моделирование фильтрации сигнала, т.е. уберём часть гармоник спектра, умножая элементы масивов  YиZ  на ординаты функции filtr(x) в соответствующих точках, изменённый спектр занесём в массивы Y1 и Z1. Таким образом, функция filtr(x)  моделирует комплексную частотную характеристику фильтра.

Анализ графика функции filtr(x) показывает, что после фильтрации в спектре останется только небольшая часть гармоник в диапазоне от 1 до 3, остальные станут равны близкими нулю, в чём можно убедиться, распечатав массивы Y1 иZ1. Таким образом можно ожидать, что  сигнал шума будет отфильтрован практически полностью, т.е. посредством функции  filtr(x) смоделировано прохождение сигнала через узкополосный активный фильтр. По виду функции filtr(x) можно также ожидать внесение искажений в исходный сигнал.

> for i to N do Y1[i]:=evalf(filtr(i)*Y[i]): Z1[i]:=evalf(filtr(i)*ZY[i]) od:

Восстановим сигнал из исходного (массивы YиZ) и изменённого (массивы Y1 иZ1) спектров, воспользовавшись процедурой обратного БПФ:

> iFFT(6,F,Z);

Распечатав массивы действительной и мнимой частей воcстановленного сигнала видим, что восстановленный сигнал несколько искажён по сравнению с исходным, при этом появилась мнимая составляющая. Таким образом мы видим, что вычисления вносят погрешность в процедуры преобразований. Важно уметь оценивать  и прогнозировать вносимую погрешность.

> #print(F,Z):

Восстановим сигнал из отфильтрованного спектра:

> iFFT(6,Y1,Z1);

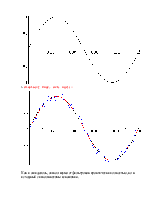
Построим графики исходного , зашумлённого  и отфильтрованного  сигналов, а затем построим эти графики на одном поле вывода:

> Sgr;

> ZSgr;

> Grb := plot ( [ Vx[n] , Y1[n]  , n = 1 .. N ] , color = black ) :

> Grb ;

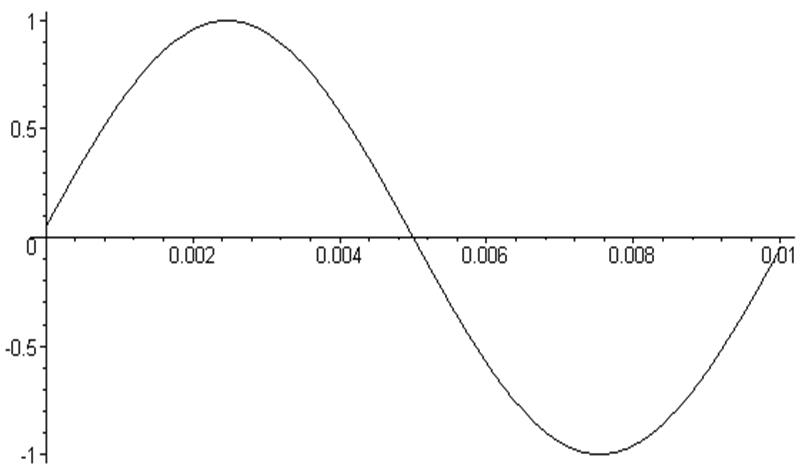
> display({ ZSgr, Grb, Sgr});

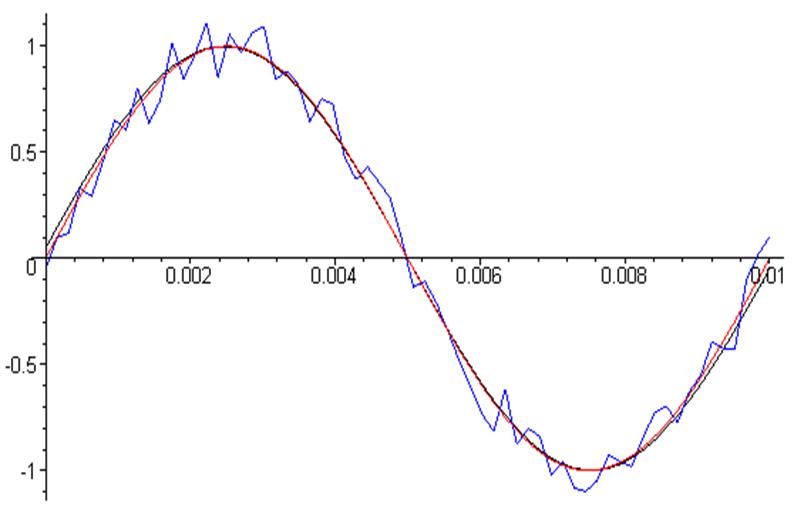
Как и ожидалось, сигнал шума отфильтрован практически полностью, но в исходный сигнал внесены искажения.

Необходимо уметь формулировать критерии качества фильтрации и выполнять по ним оценку.