





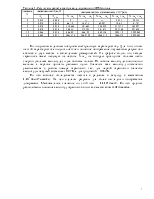



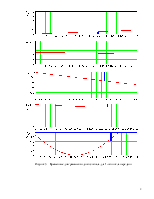
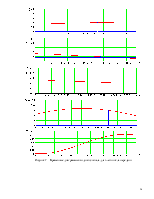






Временные диаграммы входного сигнала для 1-ого цикла передачи
Расчёт величины отсчёта при n=2 и i=0:
U1(t) = 0.9×cos(2×3.14×500×(2.955.10-6+94.56.10-6)) = 0.861 B;
U2(t) = 1.3×sin(2×3.14×713×(2.955.10-6+94.56.10-6)) = 0.534 B;
U3(t) = 1.5×cos(2×3.14×925×(2.955.10-6+94.56.10-6)) = 1.279 B;
U4(t) = -0.2×sin(2×3.14×647×(2.955.10-6+94.56.10-6)) = -0.075 B;
U5(t) = -0.4×cos(2×3.14×3200×(2.955.10-6+94.56.10-6)) = -0.378 В;
U6(t) = -3×sin(2×3.14×6400×(2.955.10-6+94.56.10-6)) = 1.842 B.
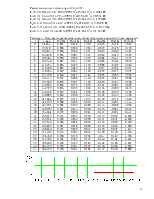
Таблица 3 – Результаты расчетов величин отсчетов входных сигналов (2 цикл передачи)
|
i |
t, мкc |
U1(t),B |
U2(t),B |
U3(t),B |
U4(t),B |
U5(t),B |
U6(t),B |
|
0 |
94.563 |
0.861 |
0.534 |
1.279 |
-0.075 |
-0.378 |
1.842 |
|
1 |
97.518 |
0.858 |
0.550 |
1.265 |
-0.077 |
-0.370 |
2.109 |
|
2 |
100.473 |
0.856 |
0.566 |
1.251 |
-0.079 |
-0.360 |
2.347 |
|
3 |
103.428 |
0.853 |
0.581 |
1.237 |
-0.082 |
-0.349 |
2.552 |
|
4 |
106.383 |
0.850 |
0.596 |
1.222 |
-0.084 |
-0.337 |
2.721 |
|
5 |
109.338 |
0.847 |
0.612 |
1.207 |
-0.086 |
-0.324 |
2.852 |
|
6 |
112.293 |
0.845 |
0.627 |
1.192 |
-0.088 |
-0.309 |
2.942 |
|
7 |
115.248 |
0.842 |
0.642 |
1.176 |
-0.09 |
-0.294 |
2.991 |
|
8 |
118.203 |
0.839 |
0.657 |
1.160 |
-0.092 |
-0.277 |
2.997 |
|
9 |
121.158 |
0.836 |
0.671 |
1.143 |
-0.095 |
-0.259 |
2.962 |
|
10 |
124.113 |
0.832 |
0.686 |
1.126 |
-0.097 |
-0.241 |
2.884 |
|
11 |
127.069 |
0.829 |
0.701 |
1.109 |
-0.099 |
-0.221 |
2.766 |
|
12 |
130.024 |
0.826 |
0.715 |
1.092 |
-0.101 |
-0.201 |
2.609 |
|
13 |
132.979 |
0.823 |
0.729 |
1.074 |
-0.103 |
-0.180 |
2.415 |
|
14 |
135.934 |
0.819 |
0.744 |
1.056 |
-0.105 |
-0.159 |
2.187 |
|
15 |
138.889 |
0.816 |
0.758 |
1.037 |
-0.107 |
-0.137 |
1.928 |
|
16 |
141.844 |
0.812 |
0.772 |
1.019 |
-0.109 |
-0.114 |
1.642 |
|
17 |
144.799 |
0.808 |
0.785 |
0.999 |
-0.111 |
-0.091 |
1.333 |
|
18 |
147.754 |
0.805 |
0.799 |
0.980 |
-0.113 |
-0.068 |
1.005 |
|
19 |
150.709 |
0.801 |
0.813 |
0.960 |
-0.115 |
-0.044 |
0.663 |
|
20 |
153.664 |
0.797 |
0.826 |
0.941 |
-0.117 |
-0.021 |
0.311 |
|
21 |
156.619 |
0.793 |
0.839 |
0.920 |
-0.119 |
0.002 |
-0.045 |
|
22 |
159.574 |
0.789 |
0.852 |
0.900 |
-0.121 |
0.027 |
-0.400 |
|
23 |
162.530 |
0.785 |
0.865 |
0.879 |
-0.123 |
0.050 |
-0.750 |
|
24 |
165.485 |
0.781 |
0.878 |
0.858 |
-0.125 |
0.074 |
-1.089 |
|
25 |
168.440 |
0.777 |
0.890 |
0.837 |
-0.126 |
0.097 |
-1.412 |
|
26 |
171.395 |
0.773 |
0.903 |
0.815 |
-0.128 |
0.120 |
-1.716 |
|
27 |
174.350 |
0.768 |
0.915 |
0.794 |
-0.13 |
0.142 |
-1.996 |
|
28 |
177.305 |
0.764 |
0.927 |
0.772 |
-0.132 |
0.164 |
-2.247 |
|
29 |
180.260 |
0.760 |
0.939 |
0.749 |
-0.134 |
0.186 |
-2.467 |
|
30 |
183.215 |
0.755 |
0.951 |
0.727 |
-0.136 |
0.206 |
-2.652 |
|
31 |
186.170 |
0.750 |
0.963 |
0.704 |
-0.137 |
0.226 |
-2.800 |
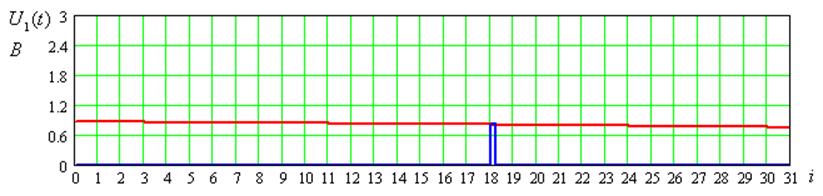
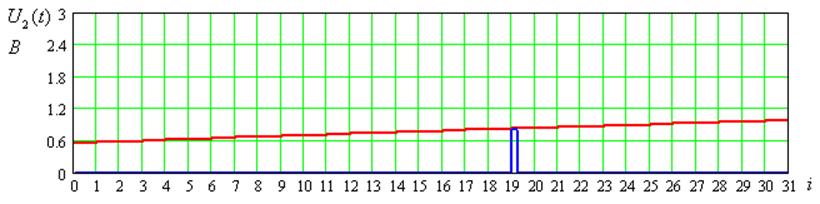
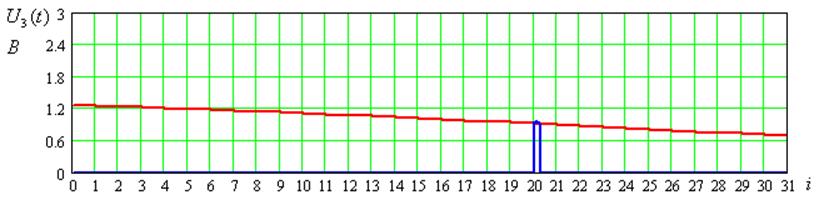
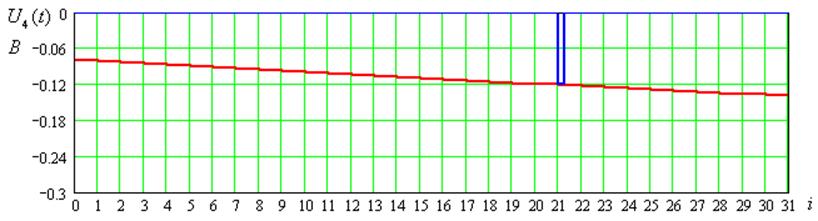
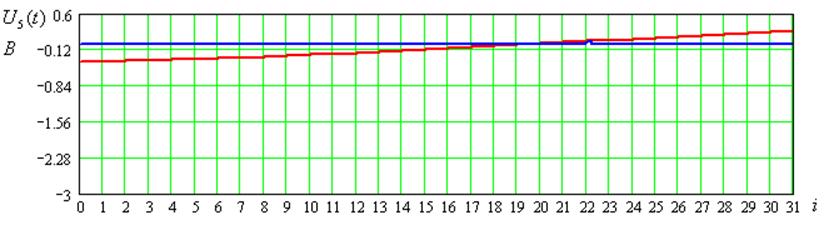
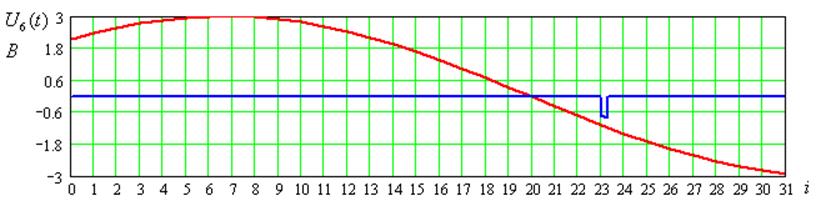
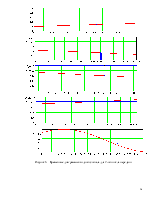
Рисунок 6 – Временные диаграммы входного сигнала для 2-ого цикла передачи
Расчет величины отсчета при n=3 и i=0:
U1(t) = 0.9×cos(2×3.14×500×(2.955.10-6+2.94.56.10-6)) = 0.746 B;
U2(t) = 1.3×sin(2×3.14×713×(2.955.10-6+2.94.56.10-6)) = 0.974 B;
U3(t) = 1.5×cos(2×3.14×925×(2.955.10-6+2.94.56.10-6)) = 0.681 В;
U4(t) = -0.2×sin(2×3.14×647×(2.955.10-6+2.94.56.10-6)) = -0.139 B;
U5(t) = -0.4×cos(2×3.14×3200×(2.955.10-6+2.94.56.10-6)) = 0.246 B;
U6(t) = -3×sin(2×3.14×6400×(2.955.10-6+2.94.56.10-6)) = -2.908 B.
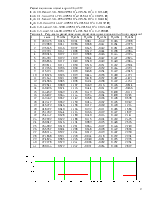
Таблица 4 – Результаты расчётов величин отсчётов входных сигналов (3-ий цикл передачи)
|
i |
t, мкc |
U1(t),B |
U2(t),B |
U3(t),B |
U4(t),B |
U5(t),B |
U6(t),B |
|
0 |
189.125 |
0.746 |
0.974 |
0.681 |
-0.139 |
0.246 |
-2.908 |
|
1 |
192.080 |
0.741 |
0.986 |
0.658 |
-0.141 |
0.264 |
-2.975 |
|
2 |
195.035 |
0.736 |
0.997 |
0.635 |
-0.142 |
0.281 |
-3.000 |
|
3 |
197.991 |
0.731 |
1.008 |
0.612 |
-0.144 |
0.298 |
-2.983 |
|
4 |
200.946 |
0.727 |
1.019 |
0.588 |
-0.146 |
0.313 |
-2.923 |
|
5 |
203.901 |
0.722 |
1.029 |
0.564 |
-0.147 |
0.327 |
-2.823 |
|
6 |
206.856 |
0.717 |
1.040 |
0.540 |
-0.149 |
0.340 |
-2.683 |
|
7 |
209.811 |
0.711 |
1.050 |
0.516 |
-0.151 |
0.352 |
-2.504 |
|
8 |
212.766 |
0.706 |
1.060 |
0.492 |
-0.152 |
0.363 |
-2.291 |
|
9 |
215.721 |
0.701 |
1.070 |
0.468 |
-0.154 |
0.372 |
-2.045 |
|
10 |
218.676 |
0.696 |
1.079 |
0.443 |
-0.155 |
0.380 |
-1.771 |
|
11 |
221.631 |
0.691 |
1.089 |
0.418 |
-0.157 |
0.387 |
-1.471 |
|
12 |
224.586 |
0.685 |
1.098 |
0.394 |
-0.158 |
0.392 |
-1.151 |
|
13 |
227.541 |
0.680 |
1.107 |
0.369 |
-0.16 |
0.396 |
-0.814 |
|
14 |
230.496 |
0.674 |
1.116 |
0.344 |
-0.161 |
0.399 |
-0.466 |
|
15 |
233.452 |
0.669 |
1.125 |
0.319 |
-0.163 |
0.400 |
-0.111 |
|
16 |
236.407 |
0.663 |
1.133 |
0.293 |
-0.164 |
0.400 |
0.245 |
|
17 |
239.362 |
0.657 |
1.142 |
0.268 |
-0.165 |
0.398 |
0.598 |
|
18 |
242.317 |
0.652 |
1.150 |
0.243 |
-0.167 |
0.395 |
0.942 |
|
19 |
245.272 |
0.646 |
1.158 |
0.217 |
-0.169 |
0.390 |
1.273 |
|
20 |
248.227 |
0.640 |
1.166 |
0.192 |
-0.171 |
0.385 |
1.586 |
|
21 |
251.182 |
0.634 |
1.173 |
0.166 |
-0.172 |
0.377 |
1.877 |
|
22 |
254.137 |
0.628 |
1.180 |
0.140 |
-0.173 |
0.369 |
2.141 |
|
23 |
257.092 |
0.622 |
1.188 |
0.115 |
-0.174 |
0.359 |
2.375 |
|
24 |
260.047 |
0.616 |
1.194 |
0.089 |
-0.175 |
0.348 |
2.576 |
|
25 |
263.002 |
0.610 |
1.201 |
0.063 |
-0.177 |
0.336 |
2.740 |
|
26 |
265.957 |
0.604 |
1.208 |
0.038 |
-0.178 |
0.322 |
2.865 |
|
27 |
268.913 |
0.597 |
1.214 |
0.012 |
-0.179 |
0.307 |
2.950 |
|
28 |
271.868 |
0.591 |
1.220 |
-0.014 |
-0.18 |
0.292 |
2.994 |
|
29 |
274.823 |
0.585 |
1.226 |
-0.040 |
-0.181 |
0.275 |
2.995 |
|
30 |
277.778 |
0.579 |
1.231 |
-0.065 |
-0.182 |
0.257 |
2.954 |
|
31 |
280.733 |
0.572 |
1.237 |
-0.091 |
-0.183 |
0.238 |
2.872 |
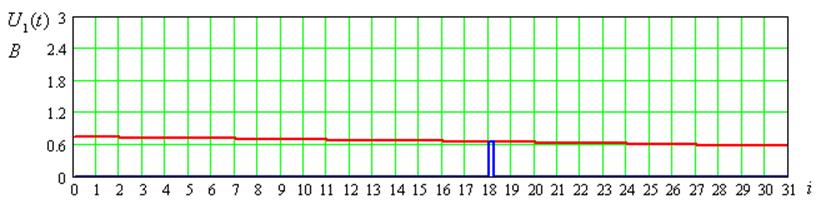
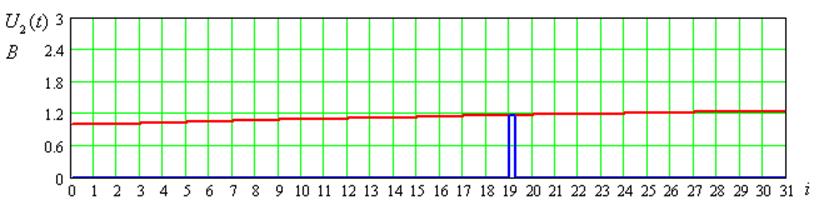
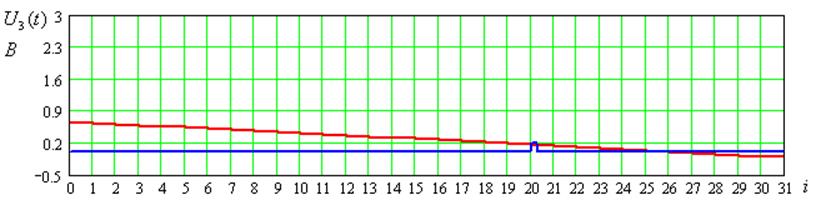
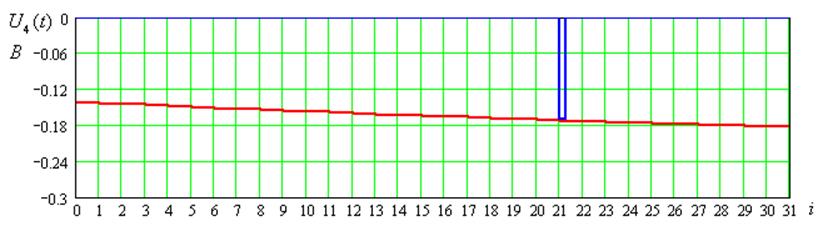
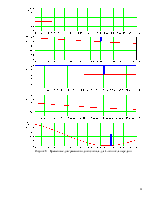
Рисунок 7 – Временные диаграммы входного сигнала для 3-его цикла передачи
Расчет величины отсчета при n=4 и i=0:
U1(t) = 0.9×cos(2×3.14×500×(2.955.10-6+3.94.56.10-6)) = 0.566 B;
U2(t) = 1.3×sin(2×3.14×713×(2.955.10-6+3.94.56.10-6)) = 1.242 B;
U3(t) = 1.5×cos(2×3.14×925×(2.955.10-6+3.94.56.10-6)) = -0.117 В;
U4(t) = -0.2×sin(2×3.14×647×(2.955.10-6+3.94.56.10-6)) = -0.183 B;
U5(t) = -0.4×cos(2×3.14×3200×(2.955.10-6+3.94.56.10-6)) = 0.219 B;
U6(t) = -3×sin(2×3.14×6400×(2.955.10-6+3.94.56.10-6)) = 2.749 B.
Таблица 5 – Результаты расчётов величин отсчётов входных сигналов (4-ый цикл передачи)
|
i |
t, мкc |
U1(t),B |
U2(t),B |
U3(t),B |
U4(t),B |
U5(t),B |
U6(t),B |
|
0 |
283.688 |
0.566 |
1.242 |
-0.117 |
-0.183 |
0.219 |
2.749 |
|
1 |
286.643 |
0.559 |
1.247 |
-0.143 |
-0.184 |
0.199 |
2.587 |
|
2 |
289.598 |
0.553 |
1.252 |
-0.168 |
-0.185 |
0.178 |
2.389 |
|
3 |
292.553 |
0.546 |
1.256 |
-0.194 |
-0.186 |
0.156 |
2.156 |
|
4 |
295.508 |
0.539 |
1.261 |
-0.219 |
-0.187 |
0.134 |
1.894 |
|
5 |
298.463 |
0.533 |
1.265 |
-0.245 |
-0.187 |
0.111 |
1.605 |
|
6 |
301.418 |
0.526 |
1.269 |
-0.27 |
-0.188 |
0.088 |
1.293 |
|
7 |
304.374 |
0.519 |
1.272 |
-0.295 |
-0.189 |
0.065 |
0.963 |
|
8 |
307.329 |
0.512 |
1.276 |
-0.321 |
-0.19 |
0.042 |
0.619 |
|
9 |
310.284 |
0.505 |
1.279 |
-0.346 |
-0.191 |
0.018 |
0.267 |
|
10 |
313.239 |
0.498 |
1.282 |
-0.371 |
-0.191 |
-0.005 |
-0.089 |
|
11 |
316.194 |
0.491 |
1.285 |
-0.396 |
-0.192 |
-0.030 |
-0.444 |
|
12 |
319.149 |
0.484 |
1.287 |
-0.42 |
-0.193 |
-0.053 |
-0.793 |
|
13 |
322.104 |
0.477 |
1.289 |
-0.445 |
-0.193 |
-0.077 |
-1.130 |
|
14 |
325.059 |
0.470 |
1.291 |
-0.47 |
-0.194 |
-0.100 |
-1.452 |
|
15 |
328.014 |
0.463 |
1.293 |
-0.494 |
-0.194 |
-0.123 |
-1.753 |
|
16 |
330.969 |
0.456 |
1.295 |
-0.518 |
-0.195 |
-0.145 |
-2.029 |
|
17 |
333.924 |
0.449 |
1.296 |
-0.542 |
-0.195 |
-0.167 |
-2.277 |
|
18 |
336.879 |
0.441 |
1.298 |
-0.566 |
-0.196 |
-0.188 |
-2.492 |
|
19 |
339.835 |
0.434 |
1.298 |
-0.59 |
-0.197 |
-0.209 |
-2.673 |
|
20 |
342.790 |
0.427 |
1.299 |
-0.614 |
-0.197 |
-0.229 |
-2.815 |
|
21 |
345.745 |
0.419 |
1.300 |
-0.637 |
-0.198 |
-0.248 |
-2.918 |
|
22 |
348.700 |
0.412 |
1.300 |
-0.66 |
-0.198 |
-0.266 |
-2.980 |
|
23 |
351.655 |
0.404 |
1.300 |
-0.683 |
-0.198 |
-0.283 |
-3.000 |
|
24 |
354.610 |
0.397 |
1.300 |
-0.706 |
-0.199 |
-0.300 |
-2.978 |
|
25 |
357.565 |
0.389 |
1.299 |
-0.729 |
-0.199 |
-0.315 |
-2.913 |
|
26 |
360.520 |
0.382 |
1.299 |
-0.751 |
-0.199 |
-0.329 |
-2.807 |
|
27 |
363.475 |
0.374 |
1.298 |
-0.773 |
-0.199 |
-0.342 |
-2.662 |
|
28 |
366.430 |
0.367 |
1.297 |
-0.795 |
-0.2 |
-0.354 |
-2.480 |
|
29 |
369.385 |
0.359 |
1.295 |
-0.817 |
-0.2 |
-0.364 |
-2.262 |
|
30 |
372.340 |
0.351 |
1.294 |
-0.839 |
-0.2 |
-0.373 |
-2.012 |
|
31 |
375.296 |
0.344 |
1.292 |
-0.86 |
-0.2 |
-0.381 |
-1.734 |
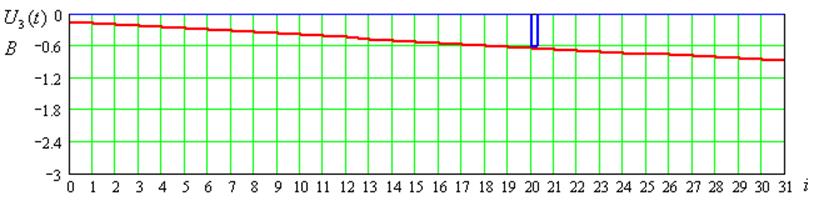
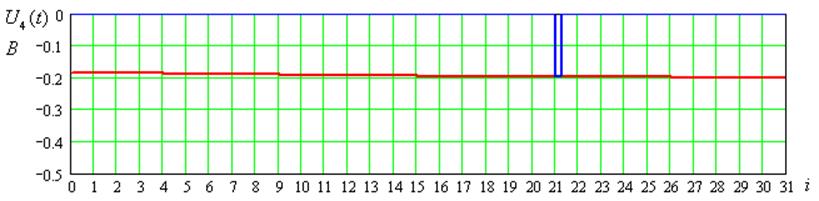
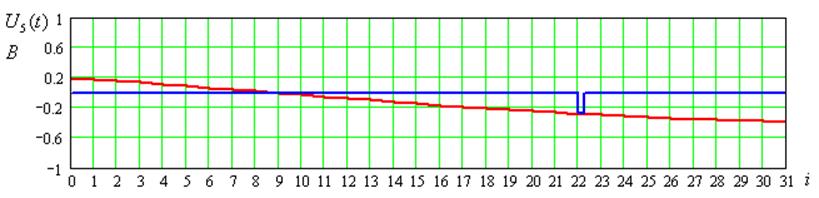
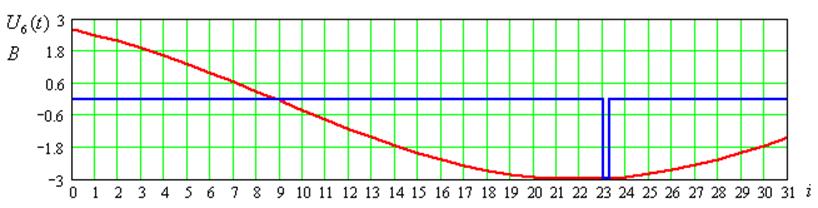
Рисунок 8 – Временные диаграммы входного сигнала для 4-ого цикла передачи
4.2 Квантование отсчётов по уровню и их кодирование
Заданная ЦСП с ИКМ использует кодер с
неравномерным шагом квантования и законом компандирования ![]() , с помощью которого получается
квазилогарифмическая характеристика компрессора.
, с помощью которого получается
квазилогарифмическая характеристика компрессора.
Нормализованная характеристика,
компрессированная с законом ![]() , определяется:
, определяется:
Fm(l) = sign(l) [ln(1 + m| l |) / ln(1 + m)];
где sign(l)- полярность;
l – амплитуда входного сигнала;
m – параметр, используемый для определения степени компрессирования.
Характеристика Fm(l) имеет особое свойство, которое заключается в возможности ее хорошей аппроксимации ломаной линией, что значительно упрощает процесс преобразования.
Значение выборки в условных единицах:
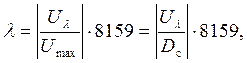
где Umax - максимальная амплитуда в условных единицах;
U - значение выборки в В;
Dc=3 - динамический диапазон сигнала.
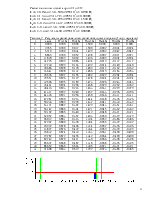
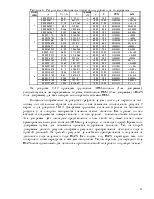
Данные, полученные в ходе расчёта, сведены в таблице 6.
Для пояснения приведём результат расчёта квантования и кодирования канала U1(t) в первом цикле в полном виде.
1) значение отсчёта: U1(t) = 0.887 В;
2)
значение выборки в условных
единицах: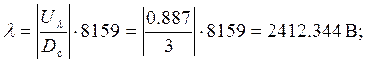
3)
номер сегмента: 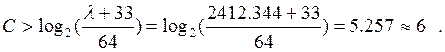
4) номер уровня квантования:
![]()
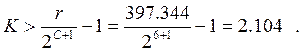
K = 3.
5) Код ИКМ: знак положителен – первый символ кода ‘1’;
С=6 – три следующие цифры кода ‘110’;
К=3 – последние четыре символа ‘0011’;
6) Код B6ZS: ‘+-+000-+’.
Таблица 6 – Результаты квантования отсчётов по уровню и их кодирование
|
Номер цикла |
ti, с |
Ui(ti), В |
li |
полярность |
Сi |
Ki |
ИКМ |
B6ZS |
|
1 |
0.000053191 |
0.887 |
2412.344 |
+ |
6.000 |
3.00 |
11100011 |
+-+000-+ |
|
0.000056147 |
0.324 |
881.172 |
+ |
4.000 |
12.00 |
11001100 |
+-00+-00 |
|
|
0.000059102 |
1.412 |
3841.165 |
+ |
6.000 |
14.00 |
11101110 |
+-+0-+-0 |
|
|
0.000062057 |
-0.05 |
135.983 |
- |
2.000 |
4.00 |
00100100 |
00+00-00 |
|
|
0.000065012 |
-0.386 |
1050.639 |
- |
5.000 |
0.00 |
01010000 |
0+0-0000 |
|
|
0.000067967 |
-0.392 |
1066.761 |
- |
5.000 |
1.00 |
01010001 |
0+0-000+ |
|
|
2 |
0.000147754 |
0.805 |
2189.583 |
+ |
6.000 |
1.00 |
11100001 |
+-+0000- |
|
0.000150709 |
0.813 |
2211.241 |
+ |
6.000 |
1.00 |
11100001 |
+-+0000- |
|
|
0.000153664 |
0.941 |
2559.534 |
+ |
6.000 |
4.00 |
11100100 |
+-+00-00 |
|
|
0.000156619 |
-0.119 |
323.645 |
- |
3.000 |
6.00 |
00110110 |
00+-0+-0 |
|
|
0.000159574 |
0.002 |
5.439 |
+ |
0.000 |
3.00 |
10000011 |
+00000-+ |
|
|
0.000162530 |
-0.400 |
1088.289 |
- |
5.000 |
1.00 |
01010001 |
0-0+000- |
|
|
3 |
0.000242317 |
0.652 |
1773.025 |
+ |
5.000 |
12.00 |
11011100 |
+-0+-+00 |
|
0.000245272 |
1.158 |
3149.268 |
+ |
6.000 |
8.00 |
11101000 |
-+-0+000 |
|
|
0.000248227 |
0.192 |
522.176 |
+ |
4.000 |
1.00 |
11000001 |
-+00000- |
|
|
0.000251182 |
-0.172 |
467.783 |
- |
3.000 |
15.00 |
00111111 |
00+-+-+- |
|
|
0.000254137 |
0.369 |
1004.527 |
+ |
5.000 |
0.00 |
11010000 |
+-0+0000 |
|
|
0.000257092 |
2.375 |
6459.221 |
+ |
7.000 |
9.00 |
11111001 |
-+-+-00+ |
|
|
4 |
0.000336879 |
0.441 |
1199.273 |
+ |
5.000 |
3.00 |
11010011 |
+-0+00-+ |
|
0.000339835 |
1.298 |
3530.157 |
+ |
6.000 |
11.00 |
11101011 |
-+-0+0-+ |
|
|
0.000342790 |
-0.614 |
1670.945 |
- |
5.000 |
10.00 |
01011010 |
0-0+-0+0 |
|
|
0.000345745 |
-0.198 |
538.494 |
- |
4.000 |
1.00 |
01000001 |
0-00000+ |
|
|
0.000348700 |
-0.266 |
723.431 |
- |
4.000 |
7.00 |
01000111 |
0-000+-+ |
|
|
0.000351655 |
-3.000 |
8159.657 |
- |
7.000 |
15.00 |
01111111 |
0-+-+-+- |
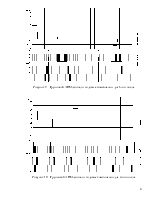
На рисунках 9-12 приведём групповые АИМ-сигналы (1-ая диаграмма), соответствующие им передаваемые кодовые комбинации ИКМ (2-ая диаграмма) и B6ZS (3-ья диаграмма) для всех четырёх циклов работы системы ИКМ.
Описание изображённых на рисунках графиков дадим только для первого из них, потому что остальные строятся аналогично и всё замечания относительно рисунка 9 верны и для рисунков 10-12. Диаграмма групповых сигналов строится на основании рисунка 5, из которого выбираются значения взятых отсчётов. Как и ранее, по оси абсцисс откладываются номера каналов i, по оси ординат – значение отсчёта в вольтах. Эта диаграмма даёт наглядное представление о том, какой вид имеет сигнал после суммирования выходных сигналов АИМ-модуляторов (т. е. на входе кодера). Кроме того, диаграмма нужна для понимания процесса кодирования сигналов. Так, на второй диаграмме данного рисунка изображён результат преобразования исходного кода в простой двоичный. На третьей - результат дальнейшего преобразования и получения из двоичного кода заданного кода B6ZS. Как видим, код B6ZS характерен тем, что полярность в нём чередуется с каждым импульсом. Таким образом, для передачи кода B6ZS необходимо иметь два источника противоположной полярности и нулевую ‘землю’.
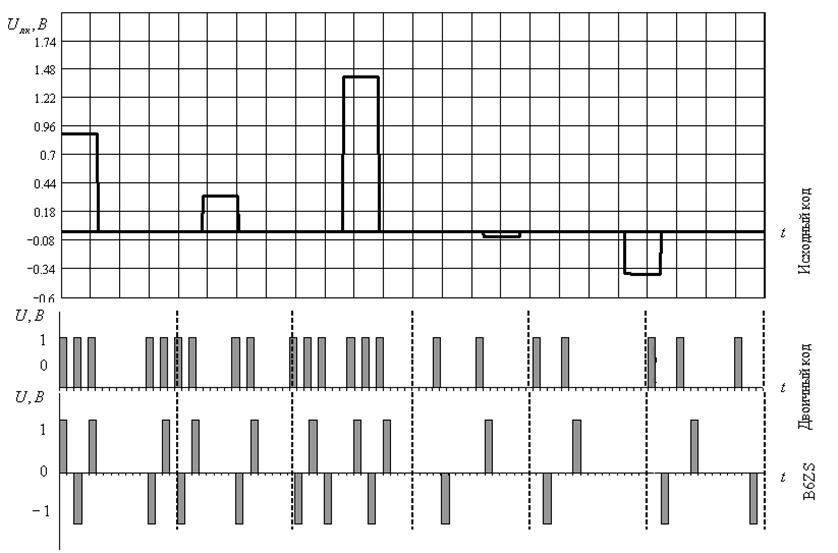
Рисунок 9 – Групповой АИМ-сигнал и кодовые комбинации для 1-ого цикла
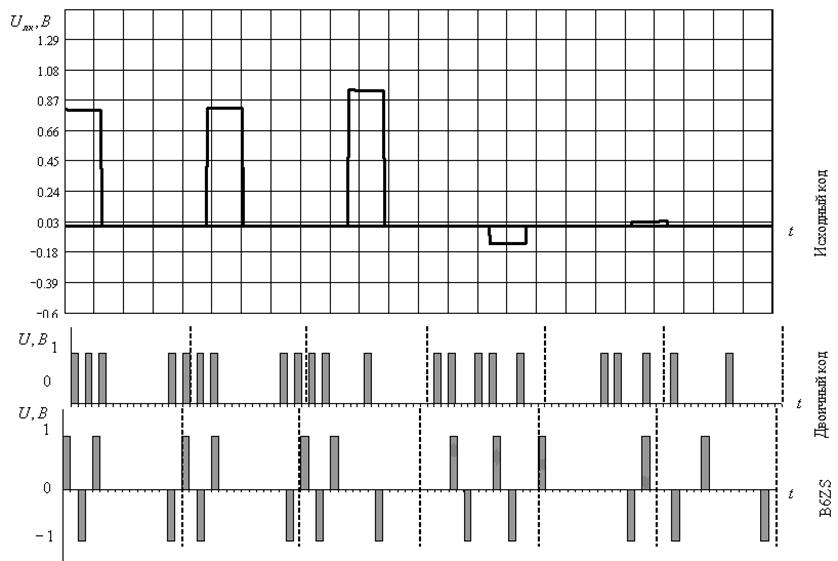
Рисунок 10 – Групповой АИМ-сигнал и кодовые комбинации для 2-ого цикла
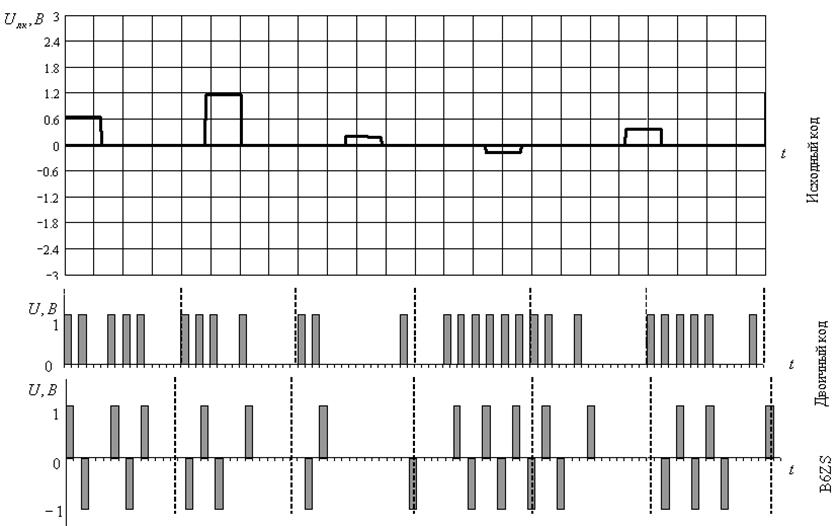
Рисунок 11 – Групповой АИМ-сигнал и кодовые комбинации для 3-его цикла
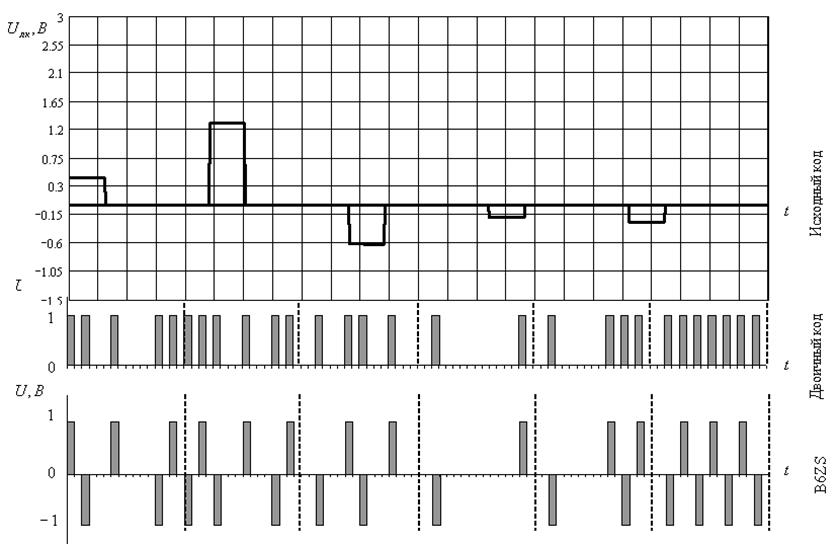
Рисунок 12 – Групповой АИМ-сигнал и кодовые комбинации для 4-ого цикла
5 АНАЛИЗ РАБОТЫ ПРИЁМНОГО УСТРОЙСТВА
В приёмном устройстве процесс декодирования происходит обратно
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.