Волна – это процесс распространения колебаний в пространстве. Упругие волны – волны, распространяющиеся в какой-то среде.
Причиной возникновения упругих волн является взаимодействие между частицами среды. Волны называются упругими, так как частицы среды пытаются вернуться в положение равновесия. Существуют поперечные (рис. 1) и продольные (рис. 2) упругие волны.
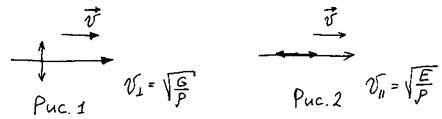
Продольные волны проходят через все среды, т.к. для них нужна упругость на сжатие. Поперечные волны проходят там, где существует упругая деформация сдвига.
E > G примерно в 2 раза, ![]()
Фронт волны – поверхность, до которой дошла волна в данный момент. Волны делятся на сферические и плоские по виду фронта.
Волновая поверхность – это поверхность одинаковых фаз.
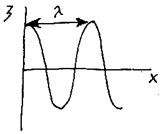
![]() - длинна волны – расстояние, которое проходит
волна за период колебания источника.
- длинна волны – расстояние, которое проходит
волна за период колебания источника.
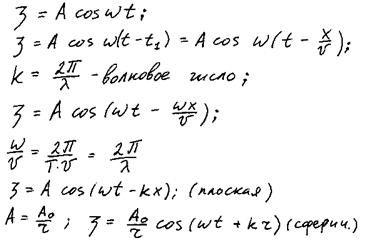
![]() - фазовая скорость – скорость
распространения волновой поверхности данной частоты. Этим понятием пользуются
для монохроматических волн.
- фазовая скорость – скорость
распространения волновой поверхности данной частоты. Этим понятием пользуются
для монохроматических волн.
2. Групповая скорость волн.
![]() -фазовая скорость;
-фазовая скорость;
![]() - дисперсионная среда;
- дисперсионная среда;
![]() - бездисперсионная среда;
- бездисперсионная среда;
![]() - групповая скорость;
- групповая скорость;
 Реально волна является
сложной, и её называют волновым пакетом.
Реально волна является
сложной, и её называют волновым пакетом.
Групповая скорость – это скорость, с которой перемещается в пространстве центр инертной волны (AMAX).
Сложный сигнал представляется в
виде набора частот монохроматических колебаний (![]() )
)
Если в среде есть дисперсия, то волновой пакет в процессе движения будет деформироваться. В бездисперсионной среде, поскольку все фазовые скорости одинаковы, деформация волнового пакета не наблюдается.
В точке C при сложении монохроматических колебаний наблюдается максимум, это значит, что волны складываются в одной фазе.
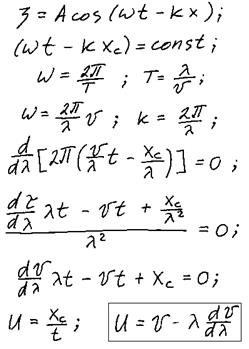
1) ![]()
2) ![]() - нормальная дисперсия;
- нормальная дисперсия;
3) ![]() - аномальная дисперсия.
- аномальная дисперсия.
3. Стоячие упругие волны
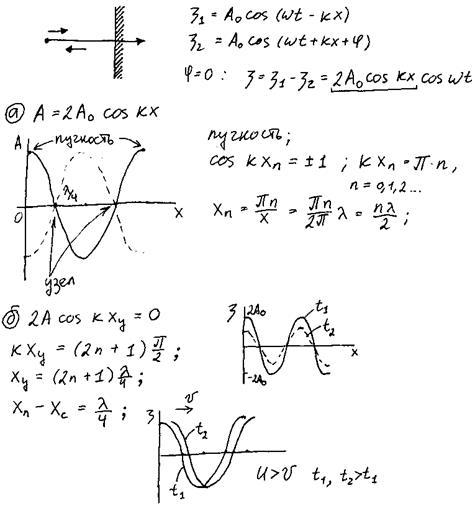
Стоячая волна в отличии от бегущей имеет амплитуду, зависящую от координаты, а у бегущей волны A=const. В стоячей волне фазы колебаний точек одинаковы. При переходе через узел стоячей волны фаза меняется на противоположную, у бегущей волны фаза меняется для разных точек с координатами X. Стоячая волна, в отличии от бегущей не переносит энергию.
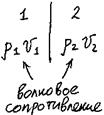 В зависимости от того, от какой среды происходит
отражение, уравнение для стоячей волны имеет разный вид.
В зависимости от того, от какой среды происходит
отражение, уравнение для стоячей волны имеет разный вид.
1) ![]() Отражение
от менее плотной среды, фаза не меняется:
Отражение
от менее плотной среды, фаза не меняется:![]()
2) ![]() Отражение
от более плотной среды, происходит изменение фазы на p:
Отражение
от более плотной среды, происходит изменение фазы на p: ![]()
Рассмотрим отражение от более плотной среды:
![]() -
фаза отраженной волны;
-
фаза отраженной волны;
![]() - это
равенство означает, что изменение фазы на p
при отражении эквивалентно потере пол (1/2) волны.
- это
равенство означает, что изменение фазы на p
при отражении эквивалентно потере пол (1/2) волны.
4. Электромагнитная волна. Скорость волны. Уравнение волны.
Уравнение бегущей электромагнитной волны:
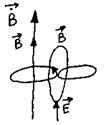
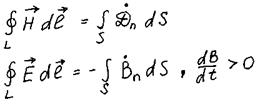
Т.к. появление переменного магнитного поля вызывает появление электрического поля q, то поля распространяются в пространстве, и если поля меняются по гармоническому закону, то в пространстве идёт электромагнитная волна.
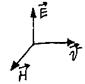
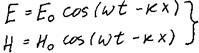 -уравнение электромагнитной
волны
-уравнение электромагнитной
волны
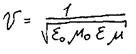 -
скорость электромагнитной волны
-
скорость электромагнитной волны
Вакуум:![]() Воздух:
Воздух:![]()

Вопрос № 5: «Энергия электромагнитной волны. Вектор Умова-Пойтинга»
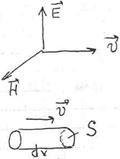 W=Wэп+Wм
W=Wэп+Wм
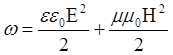
Вводится понятие потока энергии волны – энергия, проходящая ч/з ед. площади сечения в ед. времени.
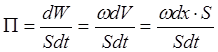
![]() – Умов эл-т
– Умов эл-т
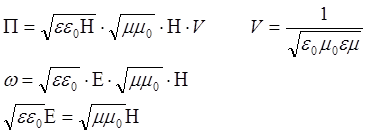
![]() (Умова-Пойтинга)
(Умова-Пойтинга)
Вопрос № 6: «Стоячие электромагнитные волны»
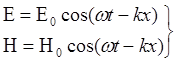 бег. вол.
бег. вол.
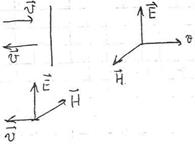 Один из векторов (вектор E или
вектор H мен-ся на противоп.)
Один из векторов (вектор E или
вектор H мен-ся на противоп.)
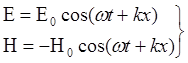
В стоячей волне фаза колебаний отличается на p/2. Пучности вектора E будет соответствовать узел вектора H.
Стоячая волна
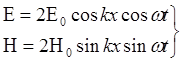
Роль границы
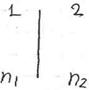

n1<n2
При отражении от оптически более плотной среды вектор E теряет половину длины волны (меняет фазу на прот.).
При отражении от оптически менее плотной среды вектор H меняет фазу на прот. (или теряет пол. длины волны).
Вопрос № 7: «Интерференция монохроматических волн»
Интерференция волн – явление сложения волн, при к-м наблюдается перераспределение энергии в пространстве (max-мы и min-мы интенсивности)
Когерентность:
 1) w1=w2
1) w1=w2
2) ![]()
3) однонапр.
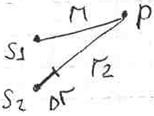
S1S2 << r1 и r2
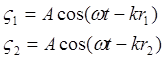 (P)
(P)
A2=A12+A22+2A1A2cosDj
Dj=k Dr
1) max Dj=2pm
Dr – разность хода A=A1+A2
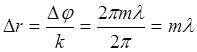
max – когда колебания в точке склад-ся в одной фазе или разность хода – целой длине волны.
2) min – в тех точках, где фазы складывающихся колебаний противоположны.
Dj=(2m+1)p
Dr=(2m+1) l/2
A=A1–A2
I~A2
max: Imax~(A1+A2)2 > I1+I2
I1~A12, I2~A22
I1+I2 ~ A12+A22
min: Imin~(A1–A2)2
I1~A12, I2~A22
I1+I2 ~ A12–A22
Imin < (I1–I2)2
Dr – геометрическая разность хода
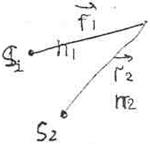 l1=l0/n1 l2=l0/n2
l1=l0/n1 l2=l0/n2
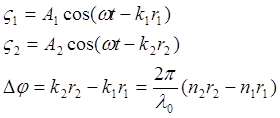
d=n2r2–n1r1 – оптическая разность хода
dmax=ml0
dmin=(2m+1)l0/2
Условие max-ма для разных сред пишут для оптич. р. х.: если d кратно целой длине l0, d - l0/2 - min
8. Когерентные источники. Временная когерентность. Методы осуществления интерференции.
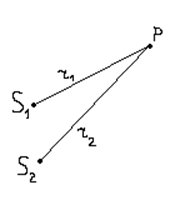
Для осуществления интерференции необходимо чтобы источники были когерентными, для этого должны выполняться следующие условия:
1) ω1 = ω2 (одинаковая частота колебаний)
2) ∆φ ≠ f(t) в точке (P) (разность фаз – постоянная величина)
3) Колебания должны быть однонаправленные (S1S2 << r1 и r2)
Так как световая волна не является монохроматической волной, меняются условия когерентности
τ -> ∆ω = 2π/τ
∆ω ≈ 1/τ
∆ωt = ∆φ(t)
Для немонохроматических источников ∆φ является функцией времени, для этого случая вводится понятие времени когерентности – это время за которое
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.