Понятие радиоактивности. Способность ядер тяжелых металлов самопроизвольно распадаться было обнаружено А.Беккерелем в 1896 г. Позднее Э.Резерфорд и супруги П. и М. Кюри показали, что атомы некоторых веществ испытывают последовательные превращения, образуя радиоактивные ряды, где каждый член ряда возникает из предыдущего, причем никакими внешними физическими воздействиями (температурой, электрическими и магнитными полями, давлением) нельзя повлиять на характеристики распада. Способность некоторых ядер самопроизвольно превращаться в другие ядра с испусканием различных видов излучения элементарных частиц называют радиоактивностью, а ядра, способные самопроизвольно распадаться, — радионуклидами. Количество ядерных превращений может быть различным, но последним элементом, ядро которого не распадается, является свинец.
Радиоактивный распад можно описать при помощи уравнений равенства сумм зарядов и массовых чисел:
![]()
где М — массовое число.
Закон сохранения массы и заряда:
М1=М2+М3; Z1=Z2+Z3
Известно четыре типа радиоактивного распада: альфа-распад; бета-распад; спонтанное деление атомных ядер (при взаимодействии медленных нейтронов); протонная радиоактивность.
Первопричиной радиоактивного распада является противоборство внутри ядра в основном двух сил: электрического отталкивания и ядерного стягивания. Носителями этих сил являются протоны. Нейтроны играют роль только стягивающих сил. Поэтому стабильность изотопа зависит от количества нейтронов в ядре. Наиболее стабильны изотопы легких элементов от гелия до меди (они содержат равное количество протонов и нейтронов). В более тяжелых элементах больше нейтронов. Однако самые тяжелые, начиная с № 82 и по № 92, также являются нестабильными, несмотря на избыток нейтронов. Например, U-238 содержит 92 протона и 146 нейтронов; распадается с периодом 4,5 млрд лет.
Альфа-распад характерен для тяжелых элементов:
![]()
![]()
следовательно, альфа-частицы — это ядра атомов гелия.
Бета-распад — это самопроизвольное испускание ядром позитронов или электронов. Электронный распад можно представить так:
![]()
где ![]() — электрон;
— электрон; ![]() — антинейтрино, т. е. нейтрон превращается
в протон.
— антинейтрино, т. е. нейтрон превращается
в протон.
Позитивный распад:
![]()
где р+ — позитрон; ![]() —
нейтрино, т. е. протон превращается в нейтрон.
—
нейтрино, т. е. протон превращается в нейтрон.
Процессы альфа- и бета-распада могут происходить и на возбужденных уровнях ядра, образовавшихся в процессе распада. Избыток энергии испускается в виде одного или нескольких гамма-квантов, например:
![]()
Превращение ядра может быть такое, как и при пози-тронном распаде, если происходит захват орбитального электрона (К-захват):
![]()
Позитронный распад и K-захват являются конкурирующими процессами. Если возможен позитронный распад, то возможен и K-захват тоже. Самопроизвольный распад тяжелых ядер возможен при захвате ими медленных нейтронов. В результате происходит деление, образуются осколки, которые могут оказаться радиоактивными, а выделенная энергия будет равна энергии связи ядра, приходящейся на одну частицу.
Гамма-излучение - это самопроизвольное испускание фотона (гамма-кванта) ядром. Оно не является самостоятельным видом радиоактивности.
Закон радиоактивного распада. Число атомов радионуклида обозначим через N, а за время dtостанется dNатомов. Тогда
dN = -λNdt, (3.1)
Где А. — коэффициент пропорциональности, называемый постоянной распада. Знак "минус" показывает, что число N исходных атомов уменьшается во времени. После интегрирования уравнения (3.1) и нормирования к исходному числу атомов Nqполучим основной закон радиоактивного распада:
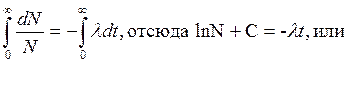
![]() (3.2)
(3.2)
где N0 — число атомов в момент времени t = 0. Скорость распада радионуклидов различна, поэтому введено понятие активности. Активность характеризует число распадов в единицу времени и равна производной по времени от уравнения (3.2):
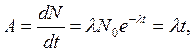 (3.3)
(3.3)
Начальная активность в момент времени t = 0 равна A0 = λN0. Тогда с учетом (3.3) можно записать:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.