Информатика и выч. техника \ Информатика

Задание на курсовую работу по дисциплине "Информатика". Требования к оформлению курсовой работы, страница 2

2. Решить задачу нахождения корней уравнения используя язык программирования Паскаль(уточнение корней уравнения может быть выполнено любым численным методом, например, методом половинного деления).Вид уравнения и точность определения корня выбрать из таблицы 3 по сумме предпоследней и последней цифр учебного шифра. Таблица 3

Сумма предпоследней и последней цифр шифра	Уравнение	Точность
0	x²+ 3 sin x = 0	0.5×10^-4
1	e^x - e^-x- 2 = 0	10^-3
2	3sin((x)¹^/²) + 0.35 x - 3.8 = 0	10^-3
3	x – 2 + sin(1/x) = 0	10^-4
4	1- х + sin х - ln (1 + x) = 0	10^-5
5	x²- ln(1 + x) - 3 = 0	10^-4
6	x-1/(3 + sin(3.6 x)) = 0	0.5×10^-4
7	ln x – x + 1.8 = 0	0.5×10^-4
8	0.1x²- x ln x = 0	0.5×10^-3
9	x + cos(x⁰^,⁵² + 2) = 0	10^-3
10	(1- 0.4x)¹^/²- arcsin x = 0	10^-3
11	x² + 10x - 10 = 0	10^-5
12	3х - 4 ln x - 5 = 0	0.5×10^-3
13	xarctg((x)^1/2) – x² = 0	10^-3
14	arccos x- (1- 0.3x³)¹^/² = 0	0.5×10^-3
15	2x - 3 ln x-3 = 0	10^-3
16	x+x^1/2+ x^3/2- 2.5 = 0	10^-4
17	e^x- (1+e^2x)^1/2- 2 = 0	0.5×10^-4
18	cos(2/x) - 2sin(1/x) +1/x = 0	0.5×10^-3
19	4x- cos x - 2 = 0	10^-4

Задача 4. Номер варианта выбрать по сумме предпоследней и последней цифр учебного шифра.

Вариант 0

Ввести по восемь значений a и b, заданных в виде прогрессий Вычислить недостающие значения

№	1	2	3	4	5	6	7	8
A
B
C
Сумму a
Сумму b
Среднее с

a1=1 ∆a=0,4 – арифметическая прогрессия, b1=1 ∆b=1,7 – геометрическая прогрессия,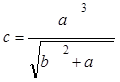

Вариант 1

Ввести по семь значений x и y, заданных в виде прогрессий Вычислить недостающие значения

№	X	y	z
1			•
2			•
3			•
4			•
5			•
6			•
7			•
Минимальное z			•
Сумма z			•

x1=1 ∆x=2,5 – арифметическая прогрессия, y1 ∆y=2,5 – геометрическая прогрессия,

Вариант 2

Ввести по семь значений x и y, заданных в виде прогрессий. Вычислить недостающие значения

№	X	Y	z
1			•
2			•
3			•
4			•
5			•
6			•
7			•
Максимальное z			•
среднее z			•

1 2 3 4 5

Скачать файл