Расчет переходных процессов в электрических цепях, страница 2

a                                                                    б

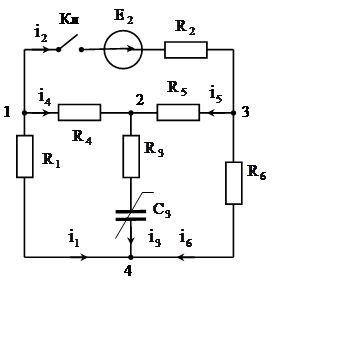
Рис. 4.3. Примеры расчетных схем к пунктам 3 и 4 задания

4. Рассчитать переходный процесс с помощью интеграла Дюамеля для указанного в карточке тока или напряжения. Для получения расчетной схемы ключ поместить в ветвь с источником ЭДС, который должен включать источник в схему после коммутации. Один из реактивных элементов необходимо закоротить в соответствии с пунктом задания, если в схеме остается емкость, то ее величина выбирается как для колебательного процесса. График напряжения источника ЭДС задается в табл.4.1 (номер графика указан в карточке задания). Значение ЭДС - задать равным значению напряжения источника из первого пункта задания, а . Значение - определить по соотношению: , а ,  и . Схема для заданного примера приведена на рис.4.3, б.

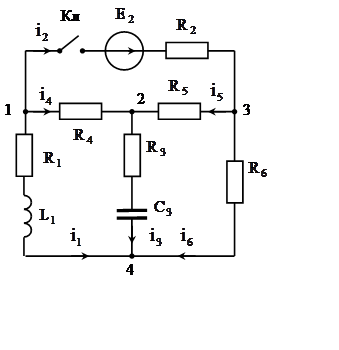
5. Рассчитать переходный процесс в нелинейной электрической цепи для указанного в п. 5 карточки задания тока или напряжения одним из следующих методов:

- кусочно-линейной аппроксимации;

- графического интегрирования;

- последовательных интервалов;

- переменных состояния.

Расчетная схема формируется из основной (рис.4.2) следующим путем: ключ помещается в ветвь с источником ЭДС и включает ее после коммутации; величина ЭДС берется из первого пункта задания; один из реактивных элементов Lили Cзакорачивается в соответствии с п. 5 карточки задания; оставшийся реактивный элемент заменяется нелинейным с заданной характеристикой. Для индуктивностизадаётся вебер-амперная характеристика y(i), в карточке - PSI и - I; для ёмкости – кулон-вольтная характеристика q(u), в карточке -Q и -U. Схема для данного примера приведена на рис.4.4, а.

6. Рассчитать частотным методом указанное в пятом пункте задания значение тока или напряжения. Ёмкость или индуктивность считать линейными элементами. Источник напряжения считается величиной постоянной и равной Е. Схема для заданного примера приведена на рис.4.4, б.

7. Рассчитать методом переменных состояния переходные процессы для токов или напряжений пунктов 1 и 2 настоящего задания.

a                                                                    б

Рис. 4.4. Примеры расчетных схем к п. 5 и 6 задания

Графики ЭДС для пункта 4 задания            Таблица 4.1, а

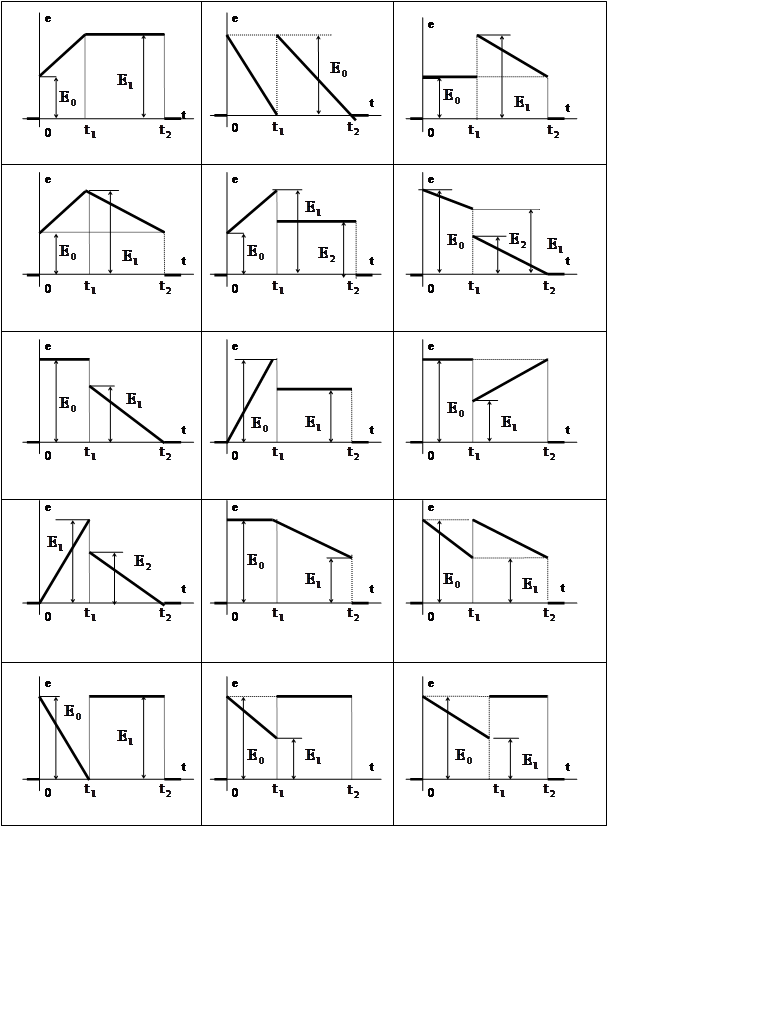Рис. 1                                      Рис. 2                                      Рис. 3

Рис. 4                                      Рис. 5                                      Рис. 6

Рис. 7                                      Рис. 8                                      Рис. 9

Рис. 10                                    Рис. 11                                    Рис. 12

Рис. 13                                    Рис. 14                                    Рис. 15

Продолжение таблицы 4.1

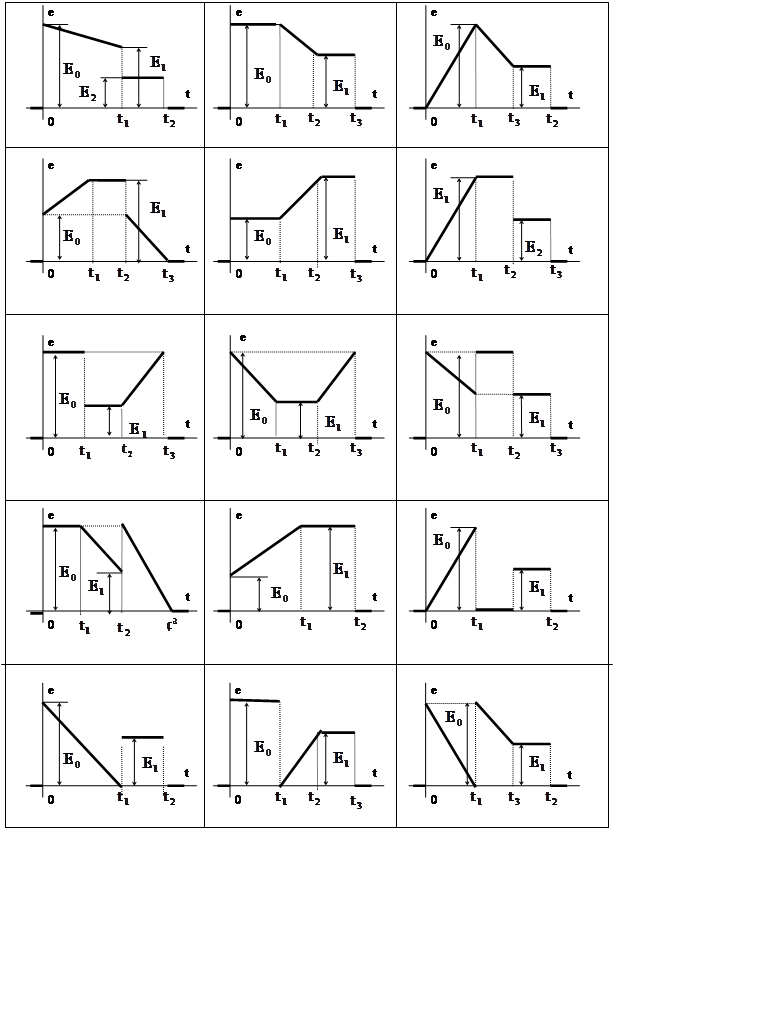Рис. 16                                    Рис. 17                                    Рис. 18

Рис. 19                                    Рис. 20                                    Рис. 21

Рис. 22                                    Рис. 23                                    Рис. 24

Рис. 25                                    Рис. 26                                    Рис. 27

Рис. 28                                    Рис. 29                                    Рис. 30

Результаты расчетов п. 1 ¸ 6 заносятся в таблицу 4.2, по которой осуществляется контроль расчета задания.

Таблица 4.2