Практический курс теоретических основ электротехники: Методическое руководство (Раздел VII: Символический метод расчета цепей синусоидального тока (метод комплексных амплитуд)), страница 2

2. Бессонов Л.А. Теоретические основы электроники. – М., 1978. – § 3.4, 3.5, 3.10 – 3.22.

ПРИМЕРЫ

Задача I

1. Представить мгновенные значения ЭДС в комплексной форме.

e₁(t) = 40 sin 314t (B)  Þ  E_1m = 40 (В);

e₂(t)  = 40 sin ( 314t – π/3) (B)  Þ  E_2m = 40е ^–j60º= 40 Ð-60⁰  (В);

e₃(t) = 40 sin (314t + 2π/3) (B)  Þ  E_3m = 40е^j120°= 40 Ð120⁰ (В).

2. Комплексы действующих значений токов имеют вид

Представить мгновенные значения этих токов.

Ответ:  

i₁(t) = 2sin (314t + 120^°) (А),   i₂(t) = 2sin (314t – 45^°) (A).

Задача 2

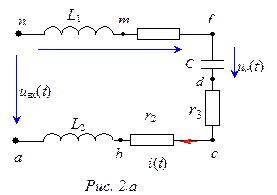В схеме (рис. 2,а):

r₁ = 6 Ом;

L₁ = 6,37 мГн;

Uk1(t)

r₂ = 4 Ом; 

L₂ =14,3 мГн;

r₃  = 5 Ом; 

С = 57,8 мкФ;

   u_вх(t) = 310 sin (ut + 60^°) B,

Рис. 2,а

     f = 200 Гц.

Рис. 2а

1. Определить ток в цепи, активную и реактивную мощность, напряжение на катушке u_к1(t), напряжение на емкости u_с(t).

2. Построить топографическую диаграмму.

Решение

1. Сопротивления реактивных элементов цепи синусоидальному току

х_L1 = ωL₁ = 2πfL₁ = 2× 3,14×200 = 8 Ом;

х_L2 = ωL₂ = 2π×f×L₂ = 18 Ом;

х_с = =  =  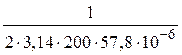= 14 Ом.

2. Комплекс действующего значения входного напряжения:

U_вх = 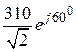= 220 Ð60 ^° (В).

3. Комплексное сопротивление цепи:

Z= r_экв + jx_экв = (r₁ + r₂ + r₃) + j(x_L1 + x_L2 – x_с) =

= (6 + 4 + 5) + j (8 + 18 – 14) = 15 + j12 = 19,2 Ð 38, 7^° (Ом).

4. Комплекс действующего значения тока:

I = 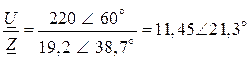  (A).

5. Мгновенное значение тока.

i(t) = 11,45sin(ωt + 21,3° )  (А).

6. Напряжение на первой катушке

     – в комплексной форме:

U_к1 = IZ_к1 = I(r₁ + jx_L1) = 11,45 Ð 21,3° ·(6 + j8) =

= 11,45 Ð 21,3⁰ ·10 Ð 53⁰ = 114,5 Ð 74,3°  (B),

     – в мгновенной форме:

u_k1(t) = 114,5sin(ωt + 74,3° )  (B).

7. Напряжение на емкости:

     – в комплексной форме:

U_C = IZ_c = I×(-jx_c) = 11,45 Ð 21,3° · 14 Ð -90^° = 160 Ð -68,7^° (B),

     – в мгновенной форме:

u_C(t) = 160sin(ωt – 68,7°) (B).

8. Комплекс полной мощности цепи:

= 220^°Ð 60° · 11,45 Ð-21,3⁰ =

= 2500 Ð 38,7° = 1955 + j1560 (BA)

9. Активная мощность цепи:

P = Re {S} = 1955 Вт.

10. Реактивная мощность цепи:

Q = Im {S} = 1560 BАp.

11. Топографическая диаграмма (рис. 2,б).

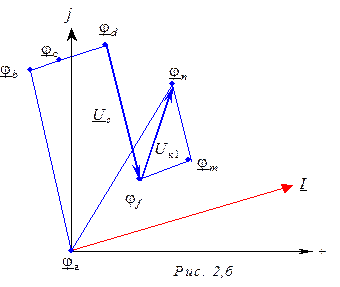
Полагаем, что j_a = 0.

Тогда

Рис. 2,б

j _b =  j _a + Ijх_L2 = 0 + 11,45Ð21,3°× 18Ð90° = 206,1Ð111,3° (B);

j_c = j_b + I r₂ = 206,1Ð111,3° + 11,45Ð21,3°× 4 = 211 ∟98,8° (B);

j _d = j _c + Ir₃ = 230,4 Ð 84,73° (B);

j _f= j _d + I(-jх_c) = 113 Ð 45° (B);

j _m = j _f + Ir₁ = 177,7 Ð 36,2°;

j _n = j _m + Ijх_L1 = 220Ð60°.

Проверка:

j _а = j _n – U = 0.

Примечание. Относительно одних и тех же точек цепи напряжение в схеме и на топографической диаграмме имеет противоположную ориентацию.

Задача 3

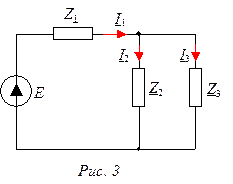
В схеме (рис. 3):

Е = 120 В;

Z₂ = 10 – j15 (Oм);

Z₃ = 2 + j6 (Ом);

Z₁  = 3,3 + j2 (Ом).

Определить комплексы и мгновенные значения токов в схеме. Составить баланс мощностей. 

Решение

1. Комплексное сопротивление цепи относительно источника:

=

==

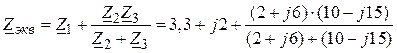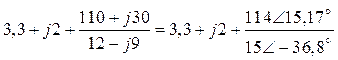= 3,3 + j2 + 7,56 Ð 51,97^º = 3,3 + j2 + 4,66 + j5,96

= 7,96 + j7.96 = 11,26 Ð 45° Ом.

2. Комплекс тока  I₁:

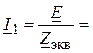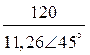–= 10,62Ð-45º(A).

3. Токи в параллельных ветвях:

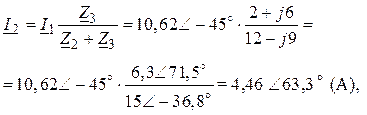
I₃ = I_{1 –} I₂ = 10,62Ð-45 º - 4,46 Ð 63,3º = 12,8 Ð-64,5º (A).

4. Мгновенные значения токов:

i₁(t) = 10,62sin(ωt – 45 º)  (A),

i₂(t) = 4,46sin(ωt+63 º20^’) (A),

i₃(t) = 12,8sin(ωt – 64 º30^’) (A).

5. Мощность источника:

= 120×10,62 Ð 45º = 1275 Ð 45 º = 904 + j904 (BA),

P_ист  = Re {S_ист} = 904 Вт

Q_ист = Im {S_ист} = 904  Вар.

6. Мощность потребителей

S_потр = ∑I²Z = I₁² Z₁ + I₂² Z₂ + I₃² Z₃ =

= 10,62²×(3,3 + j2) + 4,46²×(10 – j15) + 12,8²×(2 + j6) =

= 912 + j902 (ВА),

P_потр = Re {S_потр} = 912 Вт,

Q_потр = Im {S_потр} = 902 Вар.

7. Баланс мощностей:         Относительная погрешность

P_ист » Р_потр                           ∆ % _P =% = 0,89 %

Q_ист » Q_потр                       ∆ % _Q =% = 0,22 %

Задача 4

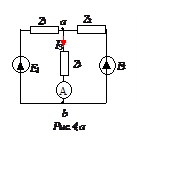В цепи (рис. 4,а)

E₁ = 127 В; 

E₂ = 127 Ð 120° B;

Z₁ = Z₂ = 1+ j3 (Ом);

Z₃ = 4+j3 (Ом).

Определить показание амперметра.

Решение

Наиболее рациональным методом определения тока I₃ является метод эквивалентного генератора:

.

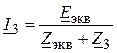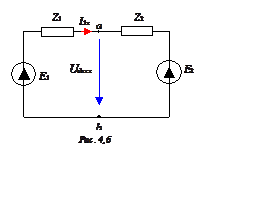
1. Комплекс внутреннего сопротивления эквивалентного генератора (рис. 4,б):

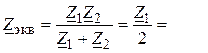
2. ЭДС эквивалентного генератора:

Е_экв = U_авхх.

Вариант А

Для выбранного направления тока I_1х (рис. 4,б)

 = E₁ – I_1xZ₁,

где

=

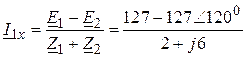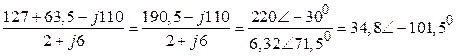= (А).

В результате,

Е_экв =  = 127 – 34,8 Ð-101,5⁰× (1 + j3) =

 = 127 – 34,8 Ð-101^°35^{’ ×}  3,16 Ð 71,5º = 31,6 + j55 = 63,4 Ð60º (B).

Вариант В

По методу двух узлов (рис. 4,б)

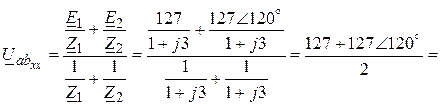
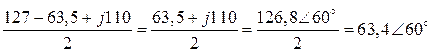=(В)

Таким образом,

Е_экв =  = 63,4 Ð60 º (В).

3.  Комплекс действующего значения тока I₃:

=.

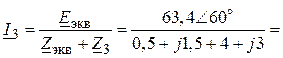
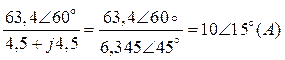4.  Показание амперметра:

A= |I₃| = 10 A

Ответ: I₃ = 10 A.

Задача 5

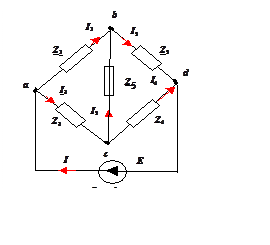Параметры схемы (рис. 5,а)

Z₁ = 10 Ом; Z₂ = j5 Ом;

Z₃ = j10 Ом; Z₄ = 5 Ом;

Z₅ = -j10 Ом.

ЭДС генератора

Е = 130 В.

Найти все токи, используя методы преобразования электрических цепей.

Построить топографиче

Рис. 5,а

                                                  скую диаграмму.

Решение

1. Для преобразования исходной цепи в последовательно-параллельную цепь целесообразно преобразовать  один из «треугольников», например, Z₁, Z₃, Z₅,  в эквивалентную «звезду» Z₁₃, Z₁₅, Z₃₅. В результате, рассматриваемая схема принимает вид, представленный на рис. 5,б с параметрами элементов:

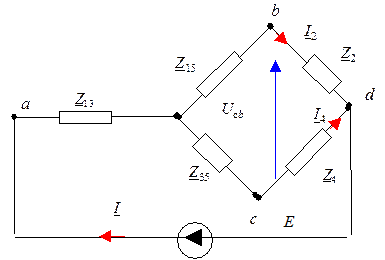
Рис. 5,6

=

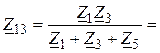
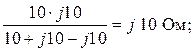
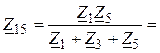
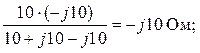
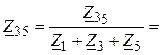
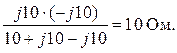
2. Ток в ветви с источником ЭДС (рис. 5,б)

=

=.

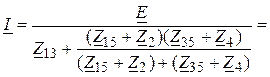
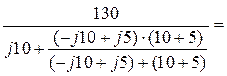
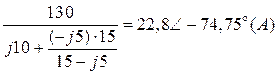3. Токи  I₂ и I₄ :

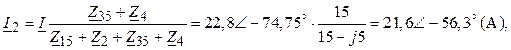
4. Ток I₅ (рис. 5,а):

I₅ = .

Как следует из рис. 5,б (второй закон Кирхгофа):

U_св = I₄Z₄ – I₂Z₂ =

= 7,2Ð-146,3° × 5 – 21,6 Ð-56,3° × j5 = 142,2Ð-146,3° (B).

В результате:

I₅ =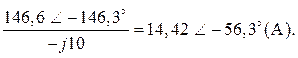

5. Остальные токи исходной цепи (рис. 5,а) определяются по первому закону Кирхгофа:

I₁ = I₂ – I₅ = 21,6Ð-56,3°– 14,42 Ð-56,3° = 7,2 Ð-56,3° (A),

I₃ = I₄ + I₅ = 7,2 Ð-146,3° +  14,42 Ð-56,3° = 16,12 Ð-82,87° (A).