Решение систем линейных алгебраических уравнений методом простой итерации, страница 2

x₃⁽¹⁾=1.205+(-3.03)*(-0.065)+(1.772)*(-0.138)+(1.094)*(-0.130)= 1.014

x₄⁽¹⁾=1.094+(-3.03)*(-0.058)+(1.772)*(-0.060)+(1.205)*(-0.083)= 1.063

Таким образом имеем

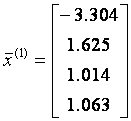
Оценка погрешности на первой итерации определяется по формуле:

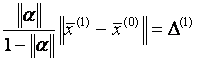
Найдем, например m-норму вектора ():

Условие не выполняется, следовательно, нужно находить приближение следующего порядка.

Результат работы программы:

Enter accuracy: 0.001 Enter number of variables: 4 Enter A: 4.72 0.48 0.07 0.33 0.24 5.68 0.63 0.74 0.46 0.98 7.08 0.92 0.53 0.55 0.76 9.13 Enter b: -14.30 10.07 8.53 9.99 Given accuracy has been riched on iteration #5. Required solution is: X0 = -3.29015 X1 = 1.65253 X2 = 1.04692 X3 = 1.09837 Press any key to exit. Press some other key to continue.

Вывод:  Я раскаиваюсь, что реализовал метод простой итерации, хотя правильнее и даже быстрее было бы реализовать метод Зейделя. Я проявил себя не с самой лучшей стороны как программист. Но таково было задание, а с работодателем, так же, как и с проверяющим лабораторные работы, спорить не желательно. Следовательно, нужно смириться с тяжкой участью программистов в наше время. А теперь вернемся непосредственно к лабораторной работе. Значит: Метод простой итерации, который мы реализовали, отличается тем, что он идеально подходит для задач, где требуется быстро найти решение, но где не требуется большая точность. Он, например, будет к месту в реализации различных алгоритмах в динамических играх, где скорость является очень критическим параметром, а погрешности из-за динамичности будут не заметны.