


НГТУ

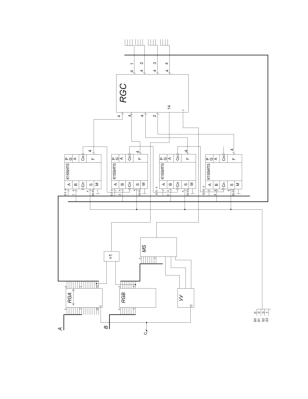
АЛУ
Факультет: АВТ Преподаватель:
Группа: АА-56 Цапенко П.М.
Студенты: Кашицын Д.В.
Смирнова Г.В.
Чумак К.А.
Новосибирск 2007
Задание:
Построить АЛУ для умножения 2-х байтовых чисел (анализ начинается с младших разрядов множителя)
Словесный алгоритм:
Необходимо осуществить перемножение 2-х 8-ми разрядных чисел.
1. Анализируем разряд множителя (начиная с младшего)
2. Если разряд равен 1, то прибавляем к сумме частичных произведений множимое. Если разряд равен 0, то к сумме частичных произведений прибавляем 0.
3. Сдвигаем влево множимое.
4. Повторим п.2-3 для всех разрядов множителя.
После того как множитель сдвигается на число разрядов, соответствующее его размерности, получим результат как конечную
сумму частичных произведений.
5. Знаки множителя и множимого объединяем по сумме модуля 2 и подается на конечную сумму частичных произведений.
|
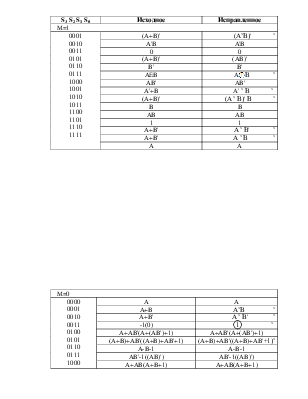
S3 S2 S1 S0 |
Исходное |
Исправленное |
|
M=1 |
||
|
0001 0010 0011 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
(A+B)' |
(AˇB)' ˇ |
|
A'B |
A'B |
|
|
0 |
0 |
|
|
(A+B)' |
(AB)' |
|
|
B' |
B' |
|
|
AEB |
A |
|
|
AB' |
AB' |
|
|
A'+B |
A' ˇ B ˇ |
|
|
(A+B)' |
(A ˇ B)' B ˇ |
|
|
B |
B |
|
|
AB |
AB |
|
|
1 |
1 |
|
|
A+B' |
A ˇ B' ˇ |
|
|
A+B' |
A ˇ B ˇ |
|
|
A |
A |
|
|
M=0 |
||
|
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 |
A |
A |
|
A+B |
AˇB ˇ |
|
|
A+B' |
|
|
|
-1(0) |
1 ˇ |
|
|
A+AB'(A+(AB')+1) |
A+AB'(A+(AB')+1) |
|
|
(A+B)+AB'((A+B)+AB'+1) |
(A+B)+AB'((A+B)+AB'+1)ˇ |
|
|
A-B-1 |
A-B-1 |
|
|
AB'-1((AB)') |
AB'-1((AB)') |
|
|
A+AB(A+B+1) |
A+AB(A+B+1) |
|
|
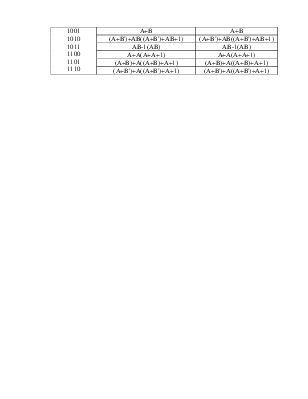
A+B |
A+B |
|
|
(A+B')+AB((A+B')+AB+1) |
(A+B')+AB((A+B')+AB+1) |
|
|
AB-1(AB) |
AB-1(AB) |
|
|
A+A(A+A+1) |
A+A(A+A+1) |
|
|
(A+B)+A((A+B)+A+1) |
(A+B)+A((A+B)+A+1) |
|
|
(A+B')+A((A+B')+A+1) |
(A+B')+A((A+B')+A+1) |
|
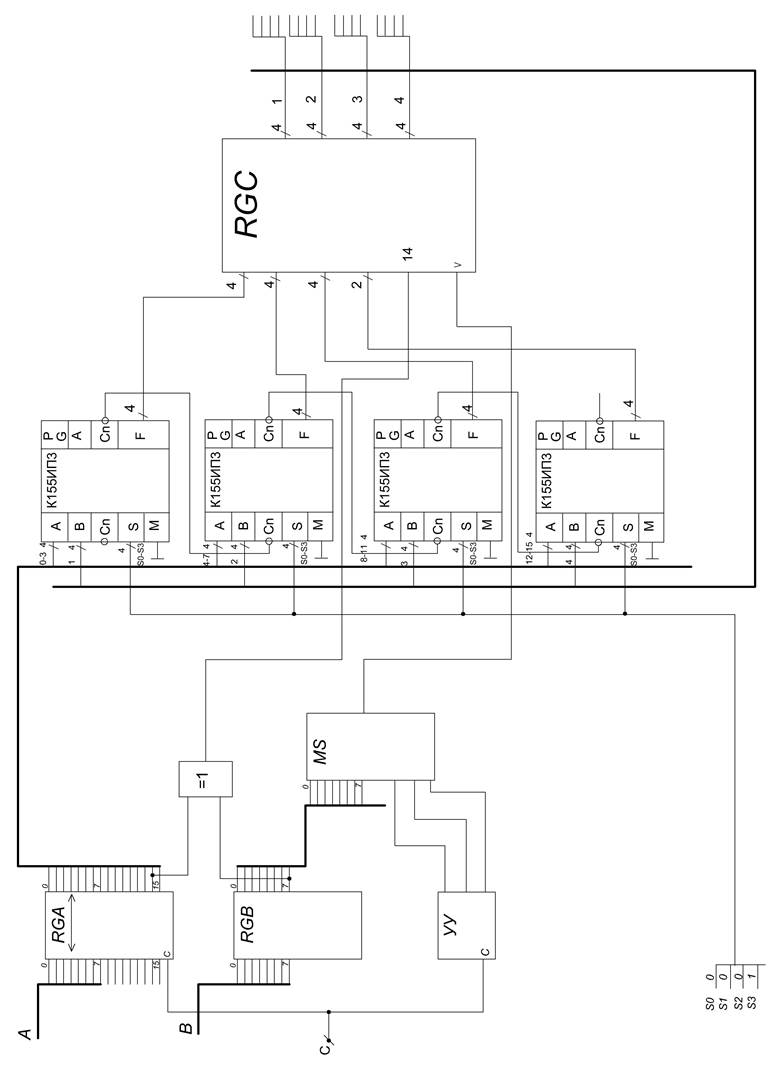
Описание на языке микрокоманд:
PrA[0-7]:=A;
PrB[0-7]:=B;
CT:=0;
M1: Если PrB[CT]=0 то перейти к M2;
PrC:= PrC+PrA;
M2: PrA:=??????? сдв…(1) PrA;
PrC:= PrC+0;
CT +1;
Если CT≠7 то перейти на M1;
Иначе Швых:=PrC;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.