Вычисление функций комплексного переменного. Матрицы, СЛАУ

Новосибирск

2008

 

Задание №1

Научиться вычислять функции комплексного переменного.

Задача:                                                                                                                                                    По придаточной функции W(s), построить амплитудно-частотную характеристику АЧХ(ω) и ее график.

Исходные данные:

K=9, T₁=0,6, T₂=0,06, T₃=0,3;

      

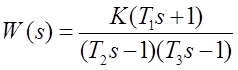
               Алгоритм:   

1.  Введем данных;

2.  Вычислим числитель и знаменатель функции W(s), учитывая что s= ω*j;

3.  Вычислим W(s) для ω [0..100] с шагом ∆ω=2, для каждого значения выделим Re{W(j ω) } и Im{W(j ω)};

4.  Вычислим

5.  Построим график АЧХ;

Ход работы:

K	T1	T2	T3	wo	∆w
9	0,6	0,06	0,3	0	2

1.   Заполним таблицу с исходными данными:

2.  Вычислим числитель (Wj(w)) и знаменатель (Pj(w)) W(w), заменив s на ω *j по соответствующим формулам:

      “=КОМПЛЕКСН(K;K*TI*C21;"j")”;

      “=КОМПЛЕКСН(1-TII*TIII*C21*C21;-TII*C21-TIII*C21;"j")”, где С21 соответствующее значение ω;

3.  Вычислим W(s) по формуле “=МНИМ.ДЕЛ(D21;E21)”           ;

4.  Выделим Re{W(j ω) } и Im{W(j ω)}по соответствующим формулам:

                                                           “=МНИМ.ВЕЩ(F21)”

                                               “=МНИМ.ЧАСТЬ(F21)”, где F21 соответствующиее значение W(s);

5.  Вычислим АЧХ по формуле “=(G21^2+H21^2)^(1/2)” и построим график АЧХ(ω);

            Тестовый пример:

i	W	Wi(w)	АЧХ
9	16	-11,4-5,6j	12,78

               Вывод:

В ходе работы я научился вычислять вычислять функции комплексного переменного Microsoft Office Excel 2003.

 

Задание №2

Научиться выполнению операций над матрицами и векторами.

Задача:                                                                                                                   

Для матрицы размером 5х5  найти наибольшую сумму элементов строки и сложить ее с матрицей.

Исходные данные:

2	3	5	6	7
4	6	5	1	2
5	4	0	4	1
3	8	2	2	2
8	6	1	5	8

               Алгоритм:   

1.Введем матрицу;

2.Найдем наибольшую сумму всех элементво всех строк;

3.К каждому элементу матрицы прибаваим полученное число в п.2.

Ход работы:

1.  Введем матрицу;

2.  Вычислим сумму элементов каждой строки по формуле:” =СУММ(C4:G4)”, где (C4:G4) соответствует диапазону строки матрицы, найдем максимальную сумму по формуле “ =МАКС(I4:I8)”, где (I4:I8) все значения сумм;

3.  К каждому элементу добавим максимальное значение суммы: “=C4+m” где С4 соответствующий элемент заданной матрицы

            Тестовый пример:

2	3	5	6	7	30	31	33	34	35
4	6	5	1	2	32	34	33	29	30
5	4	0	4	1	33	32	28	32	29
3	8	2	2	2	31	36	30	30	30
8	6	1	5	8	36	34	29	33	36

               Вывод:

В ходе работы я научился находить наибольшую сумму элементов строк матрицы 5х5 и прибавлять ее к каждому элементу матрицы в программе Microsoft Office Excel 2003.

 

Задание №3

Научиться решать квадратные уравнения.

Задача:

Для произвольного квадратного уравнения определить его корни.

Исходные данные:

               Алгоритм:   

1.Введем квадратное уравнение;

2.Определим его корни;

Ход работы:

1.Заполним таблицу для вычислений;

2.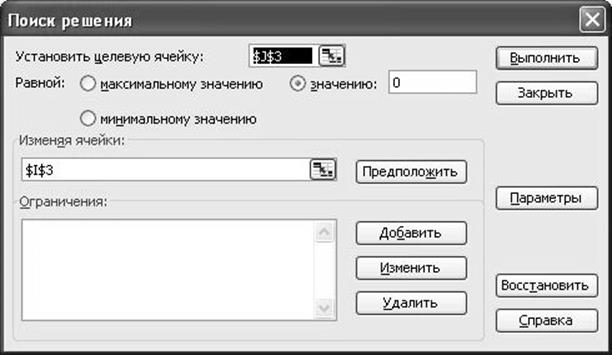В мастере “Поиск решений” сделаем следующие настройки:

Где $J$3 ячейка содержащая “=F3*I3*I3+G3*I3+H3”,где F3-a, G3-b, H3-c, I3-x;

Тестовый пример:

a	b	c	x	y
1	2	1	-1	0

Вывод: В ходе работы я научился решать квадратные уравнения в программе Microsoft Office Excel 2003.

 

Задание №4

Научиться решать системы линейных алгебраических уравнений.

Задача:  

Для произвольной системы из трех уравнений с термя неизвестными определить решение.

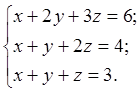Исходные данные:

               Алгоритм:   

1.Введем исходные данные;

2.Найдем значения x, y, z удовлетворяющие системе.

Ход работы:

1.Заполним таблицу с исходными данными:

a1	1	b1	2	c1	3	d1	6
a2	1	b2	1	c2	2	d2	4
a3	1	b3	1	c3	1	d3	3

2.Создадим таблицу вычислений:

		x	y	z
d1	6	1	1	1
d2	4
d3	3

3.В мастере поиск решений сделаем следующие настройки:

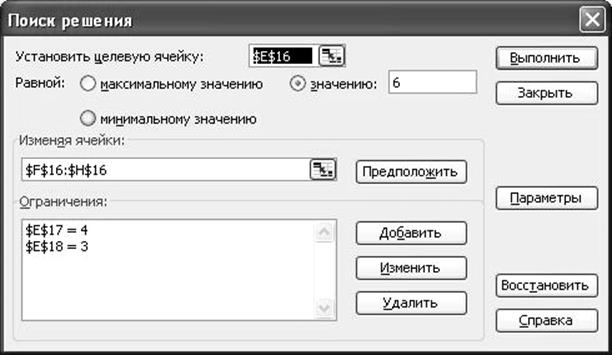
где E16-ячейка содержащая d₁, E17-d₂, E18-d₃;

Тестовый пример:

a1	1	b1	2	c1	3	d1	6	x	1
a2	1	b2	1	c2	2	d2	4	y	1
a3	1	b3	1	c3	1	d3	3	z	1

Вывод: В ходе работы я научился решать системы линейных уравнений в программе Microsoft Office Excel 2003.