Тематические тесты по дисциплине "Экономико-математические методы и модели" (Основы моделирования социально-экономических систем. Модели анализа инвестиционных проектов), страница 11

4)  среднее время обслуживания одной заявки

5)  число каналов в системе

Вопрос 16. В чем заключается свойство ординарности?

1)  в том, что заявки прибывают в систему через равные промежутки времени;

2)  в том, что обслуживающие устройства никогда не выходят из строя;

3)  в том, что среднее число заявок, поступающих в систему в единицу времени, постоянно;

4)  В том, что

5)  В том, что

6)  В том, что в один момент времени не могут поступить две и более заявок.

Тема 7.  Матричные игры

1.  Лотерея является примером:

a)  игры с нулевой суммой

b)  игры с ненулевой суммой

c)  парной игры

d)  это вообще не игра

2.  Парная игра, в которой выигрыш одного игрока равен проигрышу другого, является:

a)  игрой с природой

b)  игрой с нулевой суммой

c)  игрой с ненулевой суммой

d)  статистической игрой

3.  Игра с природой иначе называется:

a)  игрой с нулевой суммой

b)  стратегической игрой

c)  статистической игрой

d)  множественной игрой

4.  Для какой цели применяется теория матричных игр?

a)  Прогнозирование развития экономического процесса

b)  Планирование комплекса взаимосвязанных работ

c)  Выбор наилучшего варианта поведения субъекта хозяйствования в конфликтной ситуации

d)  Комплексная оценка торговых объектов

5.  Пусть дана платежная матрица:

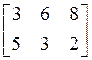
Выделенный элемент имеет смысл:

a)  стоимость перевозки единицы продукции от поставщика 1 к потребителю 3

b)  номер стратегии, которую следует выбрать игроку А

c)  Выигрыш игрока А, если игрок А выбирает первую стратегию

d)  Проигрыш игрока В, если он выбирает третью стратегию

e)  Выигрыш игрока А и, в то же время, проигрыш игрока В, при условии, что игрок А выбирает первую стратегию, а игрок В – третью стратегию

f)  Вероятность выигрыша в игре игроком А

6.  Чему равна нижняя цена игры:

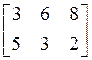
a)2  b)3c)5 d)8  e)27

7.  Чему равна верхняя цена игры:

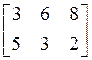
a)2  b)3c)5 d)8  e)27

8.  Что показывает нижняя цена игры?

a)  гарантированный минимальный выигрыш игрока А при любом поведении В

b)  средний выигрыш игрока А, приходящийся на одну партию

c)  гарантированный максимальный выигрыш игрока А при любом поведении В.

d)  сумма, поставленная на кон всеми участниками игры

e)  минимальная цена лотерейного билета

9.  Когда можно утверждать, что игра имеет седловую точку?

a)  Когда количество стратегий игроков А и В одинаково

b)  Когда равны выигрыши игроков А и В

c)  Когда выигрыш игрока А равен проигрышу игрока В

d)  Когда равны нижняя и верхняя цена игры

10.  Что дает игроку В его минимаксная стратегия

a)  Она гарантирует выигрыш, не меньший нижней цены игры

b)  Она гарантирует проигрыш, не больший верхней цены игры

c)  Она гарантирует максимальный выигрыш

d)  Она гарантирует минимальный проигрыш

11.  Какая парная игра является игрой с нулевой суммой?

a)  игра, для которой нижняя и верхняя цена игры равны

b)  игра, в которой выигрыш одного игрока равен проигрышу другого

c)  игра, в которой сумма выигрышей игрока А равняется 0

d)  игра, в которой сумма проигрышей игрока В равняется 0

12.  В теории игр совокупность внешних обстоятельств, в которых сознательному игроку приходится принимать решение, называется:

a)  стратегия

b)  конфликтная ситуация

c)  погода

d)  природа

e)  экономическая ситуация

13.  В чем суть принципа минимакса?

a)  выигрыш одного игрока равен проигрышу другого

b)  один из игроков безразличен к результату игры

c)  каждый из игроков должен рассчитывать на самое неблагоприятное поведение противника

d)  нижняя цена игры равна верхней

e)  отрицательный выигрыш означает на самом деле проигрыш

f)  седловая точка определяет оптимальные стратегии игроков