МИНИМИЗАЦИЯ ЗАТРАТ ПРЕДПРИЯТИЯ
1. Оптимизация использования производственных ресурсов
Один и тот же производственный результат может быть достигнут при различном сочетании производственных факторов, например труда и капитала. Если нет ограничений по использованию ресурсов и задан объем производства, то задача определения оптимального соотношения используемых производственных ресурсов — это задача определения условного экстремума функции производственных затрат: если заданы ограничения по использованию ресурсов и необходимо максимизировать прибыль предприятия — это задача линейного программирования. Для случая использования двух производственных факторов она может быть решена графическим способом: для случая использования более двух производственных факторов необходимо использовать симплекс-метод. Порядок оптимизации использования производственных ресурсов для указанных выше случаев поясняется далее на примерах решения задач.
1.1. Аналитический способ решения задач
Задача 1
Дано:
Разрабатывается месторождение. Необходимо пробурить 20 скважин. Производственная функция выглядит следующим образом:
n = 4Х11/2 Х23/2,
где п - число пробуренных скважин;
Х1 - число часов работы бригады;
Х2 - число буровых установок.
Зарплата бригады в час -300 $.
Стоимость буровой установки - 5000 $.
Определить оптимальное количество производственных факторов из условия минимума издержек производства (С).
Решение:
Математическая формулировка задачи:
С = 300Х1 +5000Х2 → min
при условии: 4Х11/2 Х23/2= 20,
20 = 4Х11/2Х23/2 ![]() Х1
=
Х1
=![]()
С = 300 ![]() + 5000Х2 =7500Х2-3
+ 5000Х2,
+ 5000Х2 =7500Х2-3
+ 5000Х2,
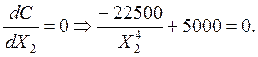 (*)
(*)
Из
уравнения (*) ![]() Х2 = 1.45, но Х2- число буровых установок (целое число)
Х2 = 1.45, но Х2- число буровых установок (целое число) ![]() Х2=1 или Х2 =2.
Х2=1 или Х2 =2.
Если Х2 = l, тo Х1 = 25 и С= 12 500.
Если Х2=2, то X1 = 3,125 и С = 10 937,5.
Ответ: Если использовать две буровые установки и задействовать бригаду рабочих на 3,125 ч, то 20 скважин будут пробурены с минимальными издержками.
1.2. Графический способ решения задач
Задача 2
Дано:
Нефтеперерабатывающее предприятие закупает нефть у двух поставщиков и производит три вида продукции (например, бензин, керосин, мазут). Относительная прибыль от продажи продуктов, полученных после переработки 1т нефти 1-го поставщика, составляет 500 руб., 2-го поставщика — 600 руб. Существуют ограничения на сбыт каждого вида продукции (см. таблицу).
|
Нефтепродукт |
1-й поставщик |
2-й поставщик |
Ограничения |
|
Бензин, т |
0,2 |
0,3 |
1,8 |
|
Керосин, т |
0,2 |
0,1 |
1,2 |
|
Мазут, т |
0,3 |
0,3 |
2,4 |
Трактовка таблицы: из 1 т нефти 1-го поставщика можно получить 0,2 т бензина, 0,2 т керосина, 0,3 т мазута и, продав эти продукты, получить прибыль 500 руб., но предприятие не может продать в день больше, чем 1,8 т бензина, 1,2 т керосина, 2,4 т мазута.
Определить: Сколько тонн нефти нужно покупать у каждого из поставщиков в день, чтобы прибыль была максимальной?
Решение:
Введем обозначения:
Q1- количество тонн нефти, купленное у 1-го поставщика;
Q2 - количество тонн нефти, купленное у 2-го поставщика.
Математическая модель задачи
Максимизируемая функция прибыли:
F= 500 Q1+600 Q2 → max.
Ограничения сбыта:
0,2 Q1 + 0,3 Q2 ![]() 1,8; (1)
1,8; (1)
0,2 Q1 + 0,1 Q2 ![]() 1,2; (2)
1,2; (2)
0,3 Q,1+ 0,3 Q2 ![]() 2,4; (3)
2,4; (3)
Q1 ![]() 0; Q2
0; Q2 ![]() 0.
0.
Задачу решаем графическим способом. На первом этапе строим область допустимых значений используемых ресурсов (рис.1). На втором этапе определяем значения функции прибыли в пограничных точках области:
FA = 3600; FВ = 4050; FС= 3000.
 |
Рис. 1 Построение области допустимых значений используемых ресурсов
В точке В значение функции прибыли максимально. Это значит, что значения О1 и О2, соответствующие точке В, являются решением задачи.
Ответ: Для максимизации своей прибыли нефтеперерабатывающее предприятие должно в день покупать 4,5 т нефти у 1-го поставщика и 3 т у
2-го поставщика.
1.3. Симплекс-метод
Ниже приведен пример решения задачи, в котором отражен формальный алгоритм симплекс-метода. Несмотря на то что в настоящее время имеется достаточно программных комплексов, реализующих симплекс-метод и от пользователя требуется лишь грамотно ввести исходные данные в симплекс-таблицу, автору пособия все таки представляется
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.