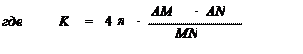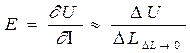Поле точечного источника. Точечный питающий электрод – электрод, радиус которого
намного меньше расстояния между питающим электродом и точкой наблюдения.
Применяемые в электрометрических методах электроды можно рассматривать, как
точечные, если поле изучается на расстояниях в пять раз превышающих глубину
заземления электрода. Глубину заземления электрода принимают равной радиусу
электрода (рис.1.3).
Дано: однородная среда, с
удельным сопротивлением –r. В нее помещен точечный
электрод. Величина стекающего тока – Ì. В однородной среде ток
стекает во все стороны равномерно.
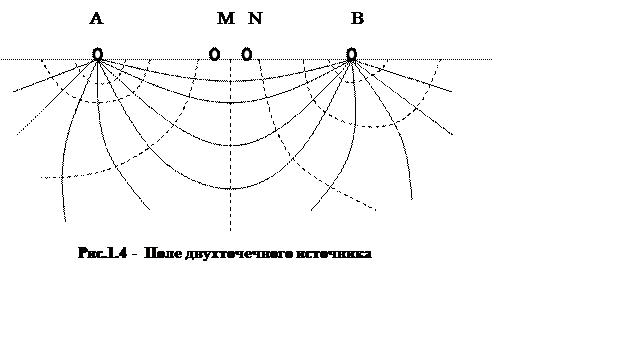
Поверхности, на которых
электрический потенциал одинаков (постоянен), называются эквипотенциальными.
Они перпендикулярны токовым линиям. Определим разность потенциалов между двумя
эквипотенциальными поверхностями, или точками, лежащими на них (точки MиN).
Приравняем правые части формул сопротивления:
DU / Ì = r×DL
/ Р.
Следует иметь в виду, что эти
формулы мы применяем сейчас не к участку тонкого линейного проводника, а к
неограниченной среде проводника. Поэтому поперечная поверхность проводника -
Р - будет поверхность сферы радиуса - r.
Р = 4p ×r2.
Расстояния AM, AN и r велики по сравнению с DL=(MN),
поэтому можно принять:
r2 =AM×AN
Находим разность потенциалов между двумя точками M
и N :




По этой формуле можно определить удельное
сопротивление среды, если известны DU, Ì и
расстояние между электродами:
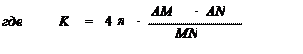
К –
коэффициент, зависящий от расстояния между электродами.
Введем новые понятия: напряженность поля
–Е,
плотность тока
– J
Закон Ома в дифференциальной форме записывается Е=j×r
Из рассматриваемой схемы
точечного источника видно, что плотность тока с увеличением радиуса до точки
измерений будет уменьшаться по закону:

![]()
![]()
![]()
![]()