Трубопроводный транспорт нефти и газа: Курс лекций (Лекции 1-17. Системы транспорта нефти и нефтепродуктов в экономике. Аварии на трубопроводах, их обнаружение и ликвидация)

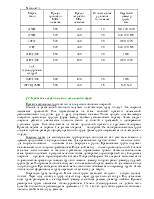
Формула Лейбензона широко применяется в тех случаях, когда зависимость ht от Q должна быть выражена в явном виде.

Величины m, А и b имеют следующие значения:

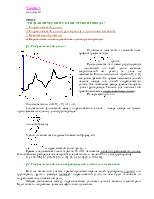
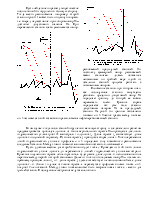
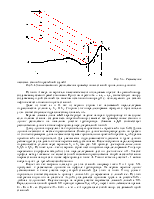
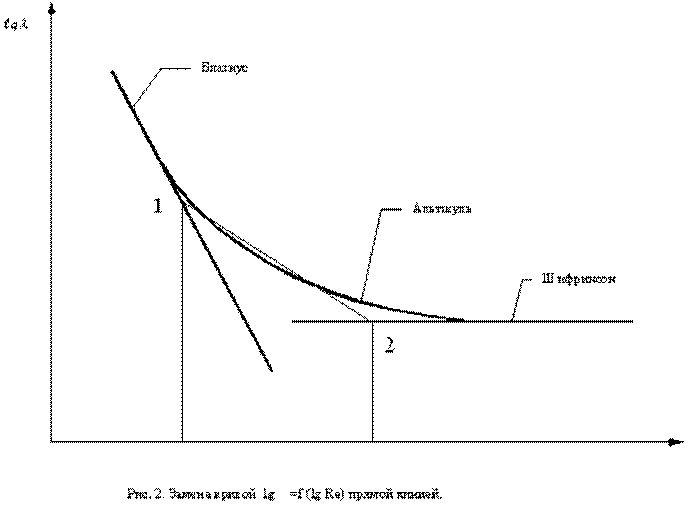
На графике lgl = f(lg Re) зависимость (6) для указанных в таблице режимов течения выглядит в виде прямых линий, тангенс угла наклона которых к оси lg Re равен m. В области смешанного трения, где l зависит не только от Re, но и от относительной шероховатости , линия lgl = f(lg Re) оказывается плавной кривой. Показатель режима течения m в этой области - переменная величина.

Последнее обстоятельство исключает возможность использования формулы Лейбензона в области смешанного трения. Это большой недостаток, так как область смешанного трения охватывает широкий интервал чисел Рейнольдса, при которых обычно ведутся перекачки маловязких нефтей и светлых нефтепродуктов. Однако, ценой некоторой потери в точности расчетов этот недостаток может быть устранен.

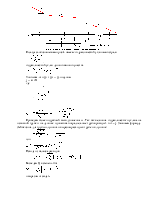
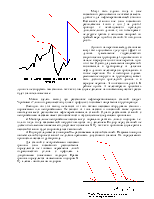
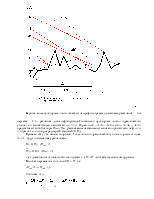
Отметим на графике lgl = f(lg Re) (рис.2) цифрой 1 точку на прямой Блазиуса, где 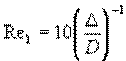, цифрой 2 точку на прямой Шифринсона, где 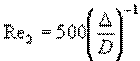(границы области смешанного трения). Подставив Re1 в формулу Блазиуса, а Re2 в формулу Шифринсона, найдем lgl 1 и lgl 2 - ординаты точек 1 и 2.

Теперь проведем через точки 1 и 2 прямую. Ее уравнение приводится к виду

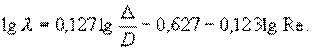
Приняв

получим

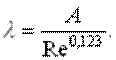(7)

Очевидно, замена кривой lgl = f(lg Re) прямой 1-2 равносильна замене формулы Альтшуля формулой (7). Это дает возможность распространить формулу Лейбензона и на область смешанного трения.

Для этой области в соответствии с (7) m = 0,123. Коэффициент b будет зависеть от (так как от зависит А). Но это не вызовет существенных неудобств при практических расчетах: величину b при заданном значении можно найти в таблице, полученной на основании приведенных выше формул.

Зависимость коэффициента b (сек2/м) от

[1, с.106-107]; [2, с.56]; [3, с. 92]; [4, с. 13-15]

Литература:

1.  Трубопроводный транспорт нефти и газа: Учебник для вузов/Р.Алиев, В.Д.Белоусов, А.Г.Немудров и др. – 2-е изд.,перераб. И доп.- М. :Недра, 1998.- 368 с.: ил.

2.  Техника и технология транспорта и хранения нефти и газа: Учеб. пособие для вузов/ Ф.Ф.Абузова, Р.А.Алиев, В.Ф.Новосёлов и др.; Под ред. В.Ф.Новосёлова. – М.: Недра, 1992. – 320 с.: ил.

3.  Агапкин В.М., Борисов С.Н., Кривошеин Б.Л. Справочное руководство по расчётам трубопроводов. – М.: Недра, 1987. – 191с.

4.  Белоусов В.Д. Технологический расчёт нефтепроводов: Учеб. пособие к курсу “Трубопроводный транспорт нефти и газа” – М.: МИНХиГП, 1977. – 68 с.

5.  Альтшуль А.Д. и др. Гидравлика и аэродинамика: Учеб. для вузов/ А.Д.Альтшуль, Л.С.Животовский, Л.П.Иванов. – М.: Стройиздат,1987, - 414 с.: ил.

6.  Лурье М.В. Сборник задач по трубопроводному транспорту нефти, нефтепродуктов и газа. – М. : ГАНГ, 1995. –267 с.

 Лекция 3

(конспект)

ТЕМА:

“ ГИДРАВЛИЧЕСКИЙ УКЛОН ТРУБОПРОВОДА”

1. Гидравлический уклон;

2. Гидравлический уклон трубопровода с лупингом и вставкой;

3. Всасывающий участок;

4. Перевальная точка и расчётная длина трубопровода.

§ 1. Гидравлический уклон.

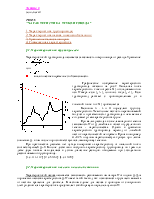
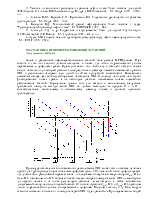
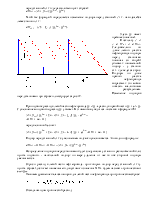
Отложим от начальной и конечной точек профиля трассы напоры

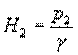и 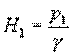(рис.3).

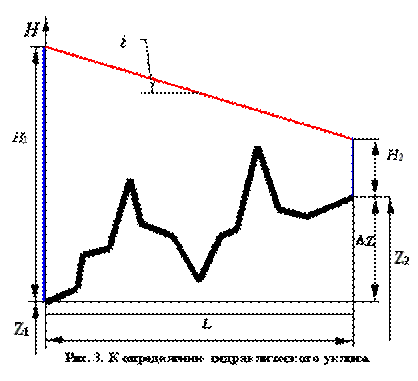
Предполагается, что диаметр трубопровода - одинаковый по всей длине, местных сопротивлений нет, расход по длине не изменяется. Концы полученных отрезков Н₁ и Н₂ соединим прямой. Эта прямая называется линией падения напора или линией гидравлического уклона. Она показывает распределение напора по длине трубопровода. Тангенс угла наклона этой прямой называется гидравлическим уклоном i.

Из чертежа видно, что

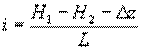
Но в соответствии с (4): Н₁ - Н₂ - D z = h.

Следовательно, физический смысл гидравлического уклона - потеря напора на трение, приходящаяся на единицу длины трубопровода:

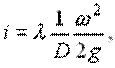
или по Лейбензону

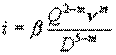
Удобно пользоваться следующей компактной формулой:

где 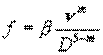- гидравлический уклон при Q = 1.

Прямая, соединяющая концы отрезков Н₁ и Н₂, называется линией гидравлического уклона. Она показывает распределение напоров (а следовательно, и давлений) по длине трубопровода.

[1, с.107-108]; [2, с.56-57]; [3, с. 93]; [4, с. 15-16]; [5, с. 100-101]

§ 2. Гидравлический уклон трубопровода с лупингом и вставкой

Если на каком-либо участке трассы проложен параллельный трубопровод (лупинг) или трубопровод другого диаметра (вставка), гидравлический уклон на нем будет отличаться от гидравлического уклона магистрали.

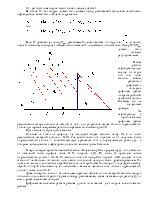
Найдем соотношения между гидравлическими уклонами лупинга, вставки и магистрали. Будет считать, что режимы движения нефти в них одинаковы.

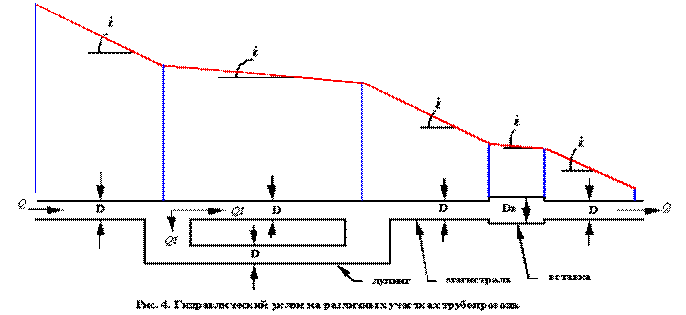
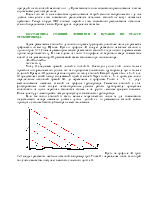
Пользуясь обозначениями рис.4, имеем: гидравлический уклон магистрали

,

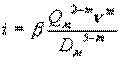гидравлический уклон лупингованного участка

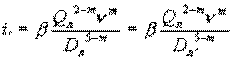
Учитывая, что Q₁ + Q₂ = Q, получим

i_л = iw             (8)

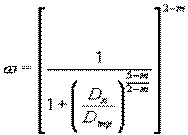
где

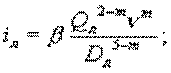
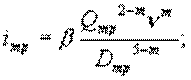
Приведём более подробный вывод значения w . Так как величина гидравлического уклона на основной трубе и на лупинге одинакова (параллельные трубопроводы), то i₁=i_л. Запишем формулу Лейбензона для трубы и лупинга и выразим расходы в трубе и в лупинге:

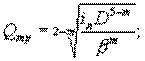
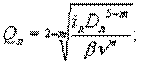
или

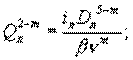
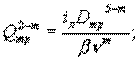
Исходя из баланса расходов

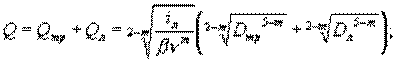
Возведём Q в степень 2-m

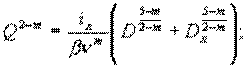
и выразим отсюда i_л

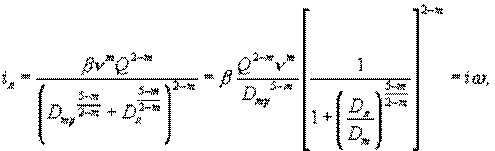
 где

 Если D_л = D_тр, то .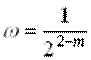

В этом случае при ламинарном режиме 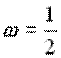, при турбулентном режиме в зоне Блазиуса w = 0,297, для квадратичной области w = 0,25.

Аналогично можно вывести для вставки

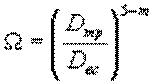
Потеря напора на трение для трубопровода с лупингом будет складываться из потерь напора на одиночном и сдвоенном (лупингованном) участках:

ht = i(L - x) + i_лx,

где х - длина лупинга.

Учитывая (8), можно также написать, что

ht = i[L - x(1 - w )].

Полная потеря напора для трубопровода с лупингом

ht = i[L - x(1 - w )] + D z                 (9)

Для трубопровода со вставкой выражение для потери напора имеет аналогичный вид.

Далее для краткости вместо (9)2 будет писать

Н = iL + D z,

имея в виду, что при необходимости всегда L можно заменить