Расчет параметров фильтрации нефти к скважине

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РЕСПУБЛИКИ БЕЛАРУСЬ

Гомельский государственный технический университет

им. П. О. Сухого

Кафедра «Гидропневмоавтоматика»

Курсовая работа

по курсу: «Подземная гидромеханика »

на тему: «Расчет параметров фильтрации нефти к скважине»

                                                  Выполнил студент гр. ЗНР – 31с

                                                  Ласица А.В.

                                                  Принял преподаватель

                                               Михневич А.В.

Гомель 2001г

Содержание

Задание...................................................................................................... 2

1.  Водонапорный режим

1.1.  Определение коэффициента совершенства скважины     4

1.2.  Определение установившегося дебита одиночной скважины для различных вариантов ее расположения в круговом пласте     5

1.3.  Оценка применимости линейного закона Дарси     7

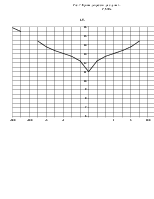
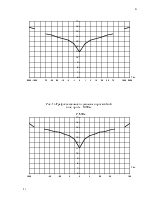
1.4.  Определение давления на различных расстояниях от скважины     11

1.5.  Определение условного отбора всей нефти из пласта     17

1.6.  Задача 1     17

1.7.  Задача 2     18

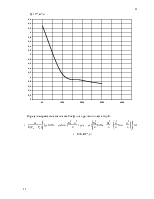
1.8.  Определение изменения распределения давления и дебита одиночной скважины, расположенной в центре кругового пласта при стягивании контура нефтеносности     21

1.9.  Определение положения фронта водонасыщенности в различные моменты времени и фронтовой водонасыщенности       26

2.  Упругий неустановившийся режим.

2.1.  Определение упругого закона нефти в пласте     27

2.2.  Определение изменения дебита скважины после пуска ее в эксплуатацию     27

2.3.  Задача 3     28

Литература.................................................................................................................... 29

Задание на курсовую работу

Рассчитать параметры фильтрации нефти к скважине при различных заданных вариантах их расположения в плоском круговом пласте с ограниченным контуром питания для водонапорного и упругого режимов работы пласта. Для этого необходимы следующие исходные данные:

-  Однородный горизонтальный круговой пласт имеет радиус контура питания R_к = 4 км.

-  Мощность пласта h = 14 м..

-  Коэффициент пористости пласта m = 0,18.

-  Коэффициент проницаемости пласта К = 0,3 Д = 0,3×1,02×10^-12 м².

-  Динамический коэффициент вязкости нефти μ_н  = 8, МПа×с;

-  Плотность нефти r = 850, ^КГ/_М³;

-  Коэффициент сжимаемости нефти b_н = 1,04×10^-9, Па;

-  Коэффициент сжимаемости породы пласта b_с = 0,72×10^-10, Па^-1;

-  Водонасыщенность нефтяного пласта s_о = 12%;

-  Коэффициент вязкости пластовой воды m_в = 1,2, МПа×с;

-  Коэффициент сжимаемости пластовой воды b_в = 4,6×10^-10, Па;

-  Пласт вскрывается скважинами на глубину в = 12, м;

-  Диаметр скважины Д_с = 24,8, см;

-  Забой скважины обсажен и перфорирован при помощи кумулятивного перфоратора. Число круглых отверстий на 1 м. – n = 10, шт.;

-  Диаметр отверстий d_о = 16, мм. Глубина проникновения пуль в породу l^/ = 100, мм.

1. Водонапорный режим.

Давление на контуре питания Р_к = 16, Мпа – постоянно. Скважины эксплуатируются при постоянном забойном давлении Р_с = 13, Мпа;

1.1. Определение коэффициента совершенства скважины.

Поскольку скважина вскрывает пласт не на всю глубину, обсажена и перфорирована, то она обладает несовершенствами: как по степени вскрытия, так и по характеру вскрытия.

Гидродинамическое несовершенство скважины учитывают при помощи коэффициента скважины d, представляющего собой отношение дебита несовершенной скважины Q к дебиту совершенной скважины в тех же условиях:

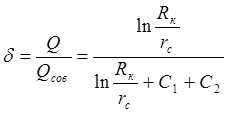
где:

R_к – радиус контура питания;

R_с – радиус скважины;

С₁ – безразмерная величина, определяющая дополнительное фильтрационное сопротивление, обусловленное несовершенством скважины по степени вскрытия пласта;

С₂ – безразмерная величина, определяющая дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по характеру вскрытия пласта.

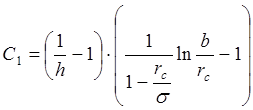- формула А. М. Пирвердяна.

Где h – относительное вскрытие пласта.

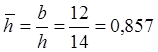
Используя формулу А. М. Пирвердяна, находим С₁:

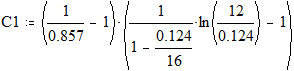
Безразмерный параметр С₂ найдем из графиков В. И. Щурова. ([1], стр. 20. рис.14):

Коэффициент совершенства скважины:

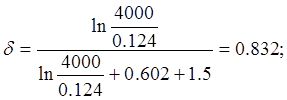
1.2. Определение установившегося дебита одиночной скважины Q для следующих вариантов ее расположения в круговом пласте.

1.  В центре;

2.  На расстоянии 0,1R_к от центра (400, м);

3.  На расстоянии 0,5R_к от центра (2000, м);

4.  На расстоянии 0,1R_к от контура (3600, м);

Рис. 1. Схема расположения скважины.

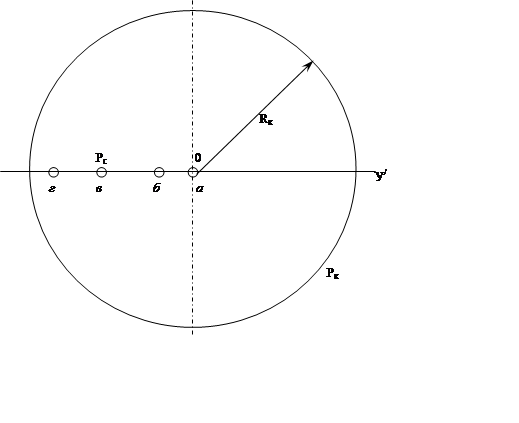Первоначально определим установившийся дебит одинокой совершенной скважины Q, эксцентрично расположенной в круговом пласте. Для этого воспользуемся формулой:

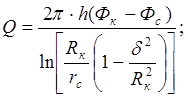
где d - расстояние от центра скважины до центра кругового пласта (эксцентриситет).

Задаемся капельной структурой потока воды и нефти, т. е. капли сравнительно крупных размеров воды (до 1 см) более-менее равномерно распределены в нефти. В связи с этим значение кажущейся вязкости жидкости принимается равной значению истинной динамической вязкости внешней фазы. В данном случае вязкости нефти. Поэтому в формуле для нахождения дебита используется вязкость нефти m_н. Результаты исчислений заносим в таблицу №1.

Таблица №1.

Зная дебиты совершенной скважины, и коэффициент совершенства несовершенной скважины определим дебиты последней: Q_несов = d×Q_сов;

1.  Q = 2,786×10^-3, м³/с;

2.  Q = 2,789×10^-3, м³/с;

3.  Q = 2,885×10^-3, м³/с;

4.  Q = 3,447×10^-3, м³/с;

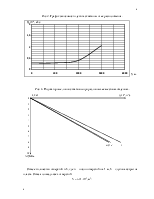
График зависимости дебита скважины от ее расположения в пласте изображен на рис. 2.

Определим коэффициенты продуктивности скважины при различных вариантах расположения скважины в пласте. Для этого используем формулу:

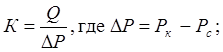
1.  К = 9,286×10^-10;

2.  К = 9,296×10^-10;

3.  К = 9,616×10^-10;

4.  К = 11,49×10^-10;

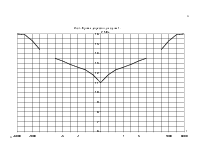
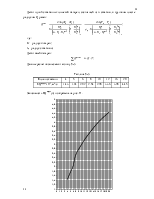
Построим индикаторные линии скважины. Зависимость дебита скважины Q от депрессии DР = Р_к – Р_с называется индикаторной линией. При плоскорадиальной фильтрации жидкости к скважине в условиях справедливости закона Дарси индикаторная линия представляет собой линию, определяющуюся уравнением:

Результаты вычислений занесем в таблицу №2.

Таблица №2.

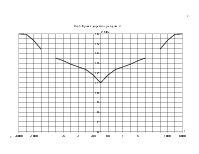
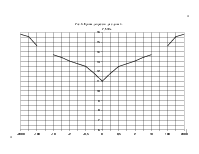
Изобразим графически индикаторные линии на рис. 3.

1.3. Оценка применимости линейного закона Дарси для рассматриваемых случаев фильтрации нефти.

Оценим применимость линейного закона Дарси по теориям Щелкачева В. Н. И Миллионщикову М. О. Перед оценкой определим площадь поверхности, через которую происходит фильтрация нефти в скважину. Т. к. скважина обсажена, и разбуривание цемента на забое не происходит, то фильтрация происходит только через