РГР № 1, задача 1. расчет многопролетной
шарнирной балки
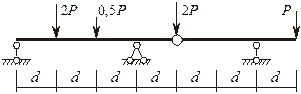
Рисунок 1
Балка состоит из двух дисков Д1 и Д2 (Д = 2), одного простого шарнира Ш (Ш = 1) и четырех опорных стержней С1 – С4 (СОП = 4) (рисунок 2).
|
Рисунок 2 |
1. Определяем степень свободы системы по формуле Чебышева W = 3Д – 2Ш – Соп = 3 × 2 – 2 × 1 – 4 = 0. Так как W = 0, балка статически определима и может быть геометрически неизменяемой. |
2. Проводим структурный анализ системы. Диск Д1 присоединен к земле при помощи трех опорных стержней С1, С2, С3, не параллельных между собой и не пересекающихся в одной точке. Следовательно, систему Д1–земля можно считать одним диском. К нему посредством шарнира Ш и стержня С4 прикреплен диск Д2, причем ось стержня не проходит через шарнир.
Таким образом, данная многопролетная балка является статически определимой, геометрически неизменяемой и неподвижно прикрепленной к земле.
Наметим расчетные сечения 1–6 (рисунок 3, а). Изобразим поэтажную схему (рисунок 3, б), в которой двухопорная балка 1–5 является основной, балка 5–8 – дополнительной.
Расчет начнем с дополнительной балки 5–8, на которую действует только заданная нагрузка. Рассматриваем ее как простую двухопорную балку (рисунок 3, в). Составим уравнения моментов относительно правой и левой опор:
∑М7 = 0; – V5 · 2d + 2P · 2d – Pd = 0, ∑М5 = 0; V7 · 2d – P · 3d = 0,
откуда V5 = (4Pd – Pd)/2d = 1,5P; V7 = 3Pd/2d = 1,5P.
Проверка: SY = V5 + V7 – 2P – P = 1,5P + 1,5P – 3P = 0.
Далее выполняем расчет основной балки 8–11, которая загружена заданной нагрузкой и сосредоточенной силой, равной соответствующей опорной реакции вышерасположенной балки 5–8: V5 = 1,5P.
Составим уравнения моментов относительно правой и левой опор:
∑М4 = 0; – V1 · 3d – V5 · d + 2P · 2d – 0,5Pd = 0,
∑М1 = 0; V4 · 3d – V5 · 4d – 2Pd – 0,5P · 2d = 0,
откуда V1 = (– 1,5Pd + 4Pd – 0,5Pd)/3d = P; V4 = (1,5P · 4d + 2Pd + Pd)/3d = 3P.
Проверка: SY = V1 + V4 – V5 – 2P – 0,5P = P + 3P – 1,5P – 2P – 0,5P = 0.
|
Рисунок 3 |
Определяем методом сечений внутренние поперечные силы и изгибающие моменты в расчетных точках, рассматривая отдельные однопролетные балки (см. рисунок 3, в). Балка 1–5. Q1 = Q2слева = V1 = P, Q2справа = V1 – 2Р = = P – 2Р = –Р, Q3справа = V1 – 2Р – 0,5Р = = Р – 2,5Р = –1,5P, Q4справа = Q5слева = V5 = 1,5P; М1 = 0, М2 = V1 · d = Pd, М3 = V1 · 2d – 2P · d = = 2Pd – 2Pd = 0, М4 = –V5 · d = –1,5Pd. Балка 5–8. Q5справа = Q6 = Q7слева = V5 – – 2Р = 1,5Р – 2Р = –0,5P, Q7справа = Q8 = P; М5 = 0, М6 = V5 · d – 2P · d = = 1,5Pd – 2Pd = –0,5Pd, М7 = –Рd, М8 = 0. Строим эпюры Q и M (рисунок 3, г). |
3 Построение линий влияния статическим методом
Для заданной многпролетной балки (рисунок 4, а) изображаем поэтажную схему (рисунок 4, б).
Линия влияния V1. Опора 1 относится к основной балке 1–5. Вначале строим линию влияния в пределах этой балки (рисунок 5, а), при этом положение силы Р = 1 задаем координатой z1, отсчитываемой от опоры 1. Составим уравнение равновесия SМ4 = 0:
1 × (3d – z1) – V1· 3d = 0, отсюда V1 = 1 – z1/3d.
Определим V1 при расположении груза Р = 1 в двух характерных точках:
![]() (груз на опоре 1),
(груз на опоре 1), ![]() (груз на опоре 4).
(груз на опоре 4).
По полученным ординатам в пределах балки 1–5 проводим прямую.
Далее продолжаем линию влияния в вышерасположенную дополнительную балку 5–8. Уже известную ординату в сечении 5 соединяем с нулевой ординатой под опорой 7. Характерные значения вычисляем из подобия треугольников. Линия влияния V1 показана на рисунке 4, в.
Линия влияния V4. Опора 4 также принадлежит основной балке 1–5. Построение ведем аналогично. Составим уравнение SМ1 = 0:
– 1 × z1 + V4 · 3d = 0, отсюда V4 = z1/3d.
![]() (груз на опоре 1),
(груз на опоре 1), ![]() (груз на опоре 4).
(груз на опоре 4).
По полученным ординатам в пределах балки 1–5 проводим прямую.
Далее уже известную ординату в сечении 5 соединяем с нулевой ординатой под опорой 7. Характерные значения вычисляем из подобия треугольников. Линия влияния V4 показана на рисунке 4, г.
|
Рисунок 4 |
Линия влияния v7. Опора 7 принадлежит дополнительной балке 5–8, поэтому линия влияния будет расположена только в ее пределах. Начало координат выберем на опоре 5, положение груза Р = 1 будем задавать координатой z2. Составим уравнение равновесия SМ5 = 0; V7 · 2d – 1 × z2 = 0, откуда V7 = z2/2d.
(груз на опоре 5),
(груз на опоре 7). По полученным ординатам строим линию влияния V7 (рисунок 4, д). |
||
|
Рисунок 5 |
Линии влияния Q2 и М2. Сечение 2 расположено между опорами основной балки 1–4, поэтому вначале построим л. в. под ней (рисунок 6, а). Рассечем балку в точке 2 (рисунок 5, б, в) и рассмотрим равновесие той ее части, на которой нет груза Р = 1 (таблица 1). Таблица 1. Построение л. в. Q2 и М2. |
||
|
Груз Р = 1 слева от сечения 2 |
Груз Р = 1 справа от сечения 2 |
||
|
SYправ. ч. = 0, Q2 = –V4. |
SYлев. ч. = 0, Q2 = V1. |
||
|
Л. в. Q2 = – л. в. V4 (левее т. 2). |
Л. в. Q2 = л. в. V1 (правее т. 2). |
||
|
SМ2прав. ч. = 0, М2 = V4 · 2d. |
SМ2лев. ч. = 0, М2 = V1 · d. |
||
|
Л. в. М2 = 2d · л. в.V4 (левее т. 2). |
Л. в. М2 = d · л. в.V1 (правее т. 2). |
||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.