Применение буферной жидкости для цементирования обсадных колонн, страница 3

W – объем всплывающей жидкости;

τ₀ – предельное натяжение сдвига среды.

  А так как при проведении экспериментов о степени влияния сил гравитации можно судить по скорости всплывания, то зависимость (1) можно выразить так:    υ = f(ρ, ρ_с, μ, μ_с, σ, D, g, W, Δρ, τ₀)      (1`)  

За основные единицы принимаем: массу – М, длину – L и время – Т.

Исходя из этого, размеренности указанных величин, выраженные через основные единицы, таковы:

[υ] = [L][T]^-1;                    [ρ] = [M][L]^-3;                 [μ] = [M][L]^-1[T]^-1;                   [σ] = [M][T]^-2;                   [D] = [L]³;                       [g] = [L][T]^-2;

[W] = [L]³;                        [τ₀] = [M][L]^-1[T]^-2        

Выберем какие-либо три параметра (по числу первоначальных основных единиц – килограмм, метр, секунда), для которых определитель Δ не равен нулю. Такими параметрами могут быть ρ, μ, g.

Для этих параметров матрица будет выглядеть так:

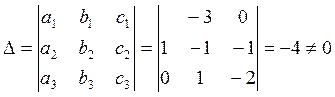  ,  [1]

 где а₁, b₁, c₁, …, a₃, b₃, c₃ – степени соответствующих размерностей.        

Это позволяет представить в общем виде критериальное уравнение процесса гравитационных перемещений в трубе.

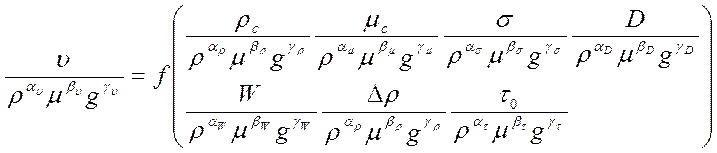  (2)

Таким образом, процесс характеризуется восьмью безразмерными критериями.

Значения α_υ, β_υ, γ_υ, … α_τ, β_τ, γ_τ определяем из условия, что входящие в выражение (2) комплексы суть безразмерные величины:

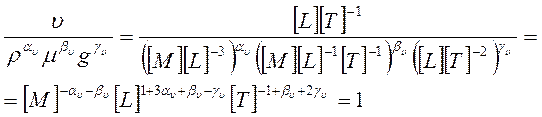
Для данного условия справедливо следующее

- α_υ – β_υ = 0,        1+3α_υ + β_υ - γ_υ = 0,

- 1 + β_υ +2γ_υ = 0,

откуда

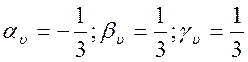
Получив эти показатели составляем первый безмерный критерий

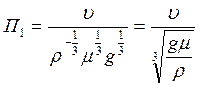
Аналогичным образом применяя метод нулевых размерностей, находим остальные безразмерные критерии:

                      

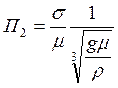
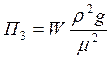
- критерий, характеризующий влияние объема всплывающей жидкости (критерий Галилея);

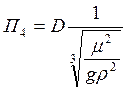
- критерий, характеризующий влияние диаметра колонны;

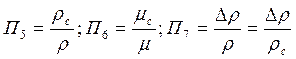
- симплекс Архимеда

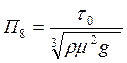
- критерий, учитывающий влияние предельного натяжение сдвига среды на всплывание жидкости.

После преобразования полученных безразмерных критериев, получаем критерии, наиболее ясно отражающие влияние на процесс гравитационного перемещения отдельных входящих в них параметров, и имеющих наиболее простой вид

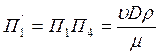
- критерий Рейнольдса (Re);

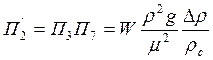
- критерий Архимеда (Ar);

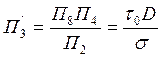
- объединенный критерий, показывающий влияние τ₀ и σ на процесс гравитационного перемещения одной жидкости в другой в стесненных условиях.

Теперь уравнение (1`) в критериальной форме можно записать в виде:

Re = f(Ar, П₃', П₄, П₂, П₅, П₆).

Для случая всплывания одной ньютоновской жидкости в другой τ₀=0 и критерий П₃' исчезает. В этом случае для учета влияния поверхностного натяжения необходимо учитывать следующий критерий:

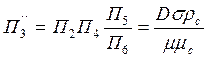
Критериальное уравнение в этом случае будет выглядеть так:

Re = f(Ar, П₃'', П₄, П₅, П₆).

3. Способы повышения эффективности использования буферных жидкостей.

Одним из важнейших вопросов в технологии бурения скважин является повышение качества цементирования обсадных колонн. В этом плане большая роль принадлежит правильному выбору состава и свойств буферной жидкости, используемой в процессе цементирования. Проведенные лабораторные исследования позволили предложить методику оценки эффективности моющих буферных жидкостей. В ее основу положен принцип изучения динамики изменения веса глинистой корки при воздействии на нее различных по составу и свойствам буферных жидкостей.

Исследования проводили на установке, позволяющей в динамических условиях следить за состоянием глинистой корки, сформированной на пористой поверхности. Процесс формирования глинистой корки осуществляли под давлением 0,981МПа в течение 30мин [3] затем ее помещали в буферную жидкость и приводили во вращение. Через определенные промежутки времени фиксировали изменение веса глинистой корки и на основании этого строили график динамики ее смыва. Результаты исследования отмывающей способности различных буферных жидкостей представлен на рис.1 [3].