














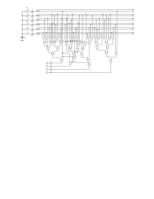
Electronic Workbench от фирмы Interactive Image Technologies Ltd. В данной работе будет использоваться версия 4.0 этой программы.
Сначала построим общую шину нашего комбинационного автомата с цепью питания. Хорошим способом проверки схемы будет подсоединение на входы ключей, которые мы можем замыкать и размыкать определёнными клавишами и лампочек-индикаторов, сигнализирующих о наличии единичного сигнала на входе. Подсоединив лампочки на выходе, мы можем совершенно точно проверить правильность нашей схемы и уравнений.
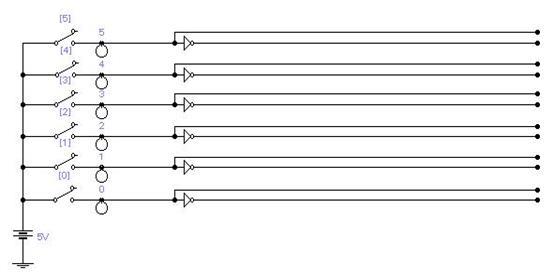
Как видно на рисунке, с помощью инверторов, мы вывели на общую шину как сами входы, так и инвертированные входы. Обратившись к таблице микросхем, мы заметим, что шесть инверторов содержится у нас в микросхеме К1533ЛН1. Аналог на западе этой микросхемы – 7405. Её и содержит в своей элементной базе Electronic WorkBench.
Элементная база позволяет нам свободно использовать следующие логические элементы:
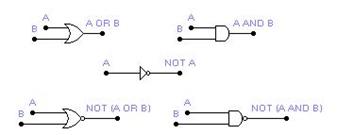
В данном варианте базис И-НЕ, поэтому мы можем использовать только последний элемент. Данный элемент содержат следующие микросхемы:
|
1533ЛА3 |
Четыре 2И-НЕ |
|
1533ЛА8 |
Четыре 2И-НЕ с открытым коллектором (элементы контроля) |
|
1533ЛА9 |
Четыре 2И-НЕ с открытым коллектором |
|
1533ЛА12 |
Четыре буферных 2И-НЕ с высокой нагрузочной способностью |
|
1533ЛА13 |
Четыре буферных 2И-НЕ с открытым коллектором и высокой нагрузочной способностью |
Наиболее распространена и доступна первая микросхема (аналог 7400 на Западе). Она содержит четыре двухвходовых элемента И-НЕ. Учитывая использование только этой микросхемы, построим реализацию Y0.
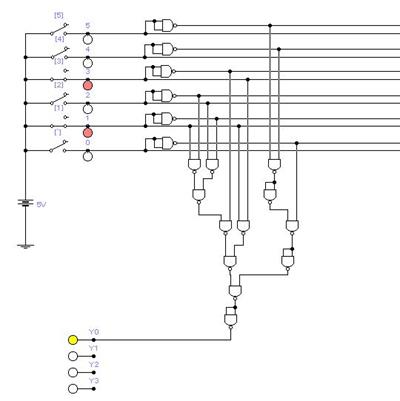
В итоге получается следующая схема для Y0. Обратите внимание, как с помощью элемента И-НЕ реализована операция И: И-НЕ-НЕ. На рисунке видна фаза проверки одного из сочетаний Х0 – Х5.
Выполним схемы для остальных Y.
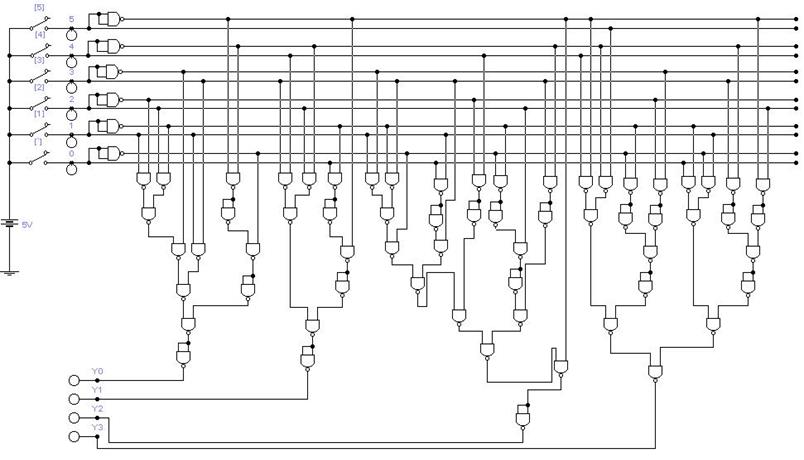
Взглянем ещё раз на систему:
![]()
![]()
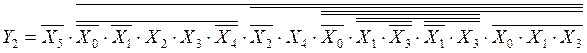
![]()
Выпишем все одиночные аргументы и одиночные инверсии аргументов, участвовавшие в уравнениях, учитывая все повторения:
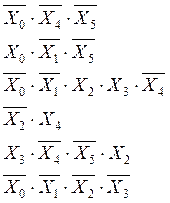
Заменив ![]() на a, а
на a, а ![]() - на b, получим небольшое сокращение схемы:
- на b, получим небольшое сокращение схемы:
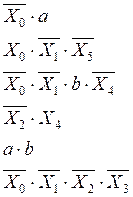
Схема сократилась на 4 элемента И-НЕ и всего в ней 65 элементов.
Конечный результат:
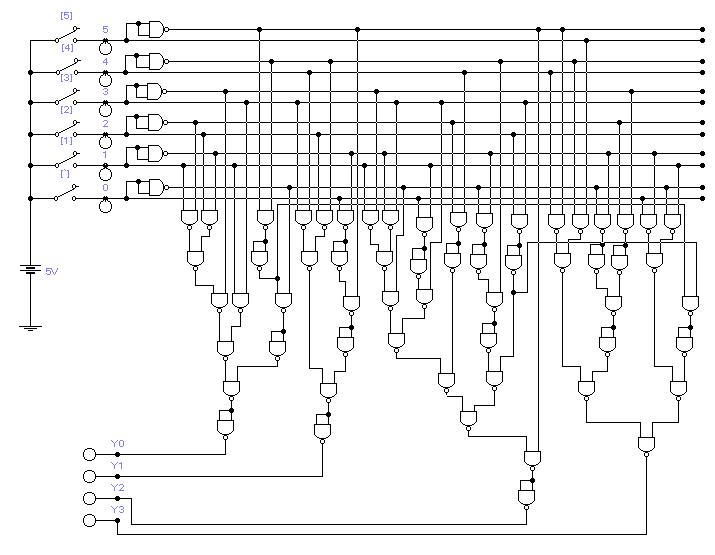
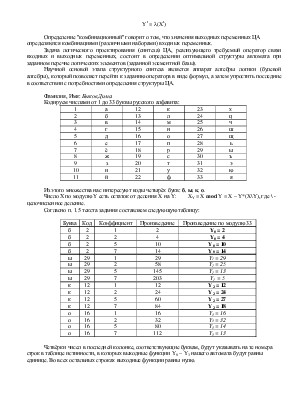
Фамилия, Имя: Кудрякова Ирина.
Кодируем числами от 1 до 33 буквы русского алфавита:
|
1 |
А |
12 |
к |
23 |
х |
|
2 |
Б |
13 |
л |
24 |
ц |
|
3 |
В |
14 |
м |
25 |
ч |
|
4 |
Г |
15 |
н |
26 |
ш |
|
5 |
Д |
16 |
о |
27 |
щ |
|
6 |
Е |
17 |
п |
28 |
ь |
|
7 |
Ё |
18 |
р |
29 |
ы |
|
8 |
Ж |
19 |
с |
30 |
ъ |
|
9 |
З |
20 |
т |
31 |
э |
|
10 |
И |
21 |
у |
32 |
ю |
|
11 |
Й |
22 |
ф |
33 |
я |
Из этого множества нас интересуют коды четырёх букв: к, у, д, р.
Число Х по модулю Y есть остаток от деления X на Y: XY = X mod Y = X – Y*(X\Y), где \ - целочисленное деление.
Согласно п. 1.5 текста задания составляем следующую таблицу:
|
Буква |
Код |
Коэффициент |
Произведение |
Произведение по модулю 33 |
|
к |
12 |
1 |
12 |
Y0 = 12 |
|
к |
12 |
2 |
24 |
Y0 = 24 |
|
к |
12 |
5 |
60 |
Y0 = 27 |
|
к |
12 |
7 |
84 |
Y0 = 18 |
|
у |
21 |
1 |
21 |
Y1 = 21 |
|
у |
21 |
2 |
42 |
Y1 = 9 |
|
у |
21 |
5 |
105 |
Y1 = 6 |
|
у |
21 |
7 |
147 |
Y1 = 15 |
|
д |
5 |
1 |
5 |
Y2 = 5 |
|
д |
5 |
2 |
10 |
Y2 = 10 |
|
д |
5 |
5 |
25 |
Y2 = 25 |
|
д |
5 |
7 |
35 |
Y2 = 2 |
|
р |
18 |
1 |
18 |
Y3 = 18 |
|
р |
18 |
2 |
36 |
Y3 = 3 |
|
р |
18 |
5 |
90 |
Y3 = 24 |
|
р |
18 |
7 |
112 |
Y3 = 27 |
Четвёрки чисел в последней колонке, соответствующие буквам, будут указывать на те номера строк в таблице истинности, в которых выходные функции Y0 – Y3 нашего автомата будут равны единице. Во всех остальных строках выходные функции равны нулю.
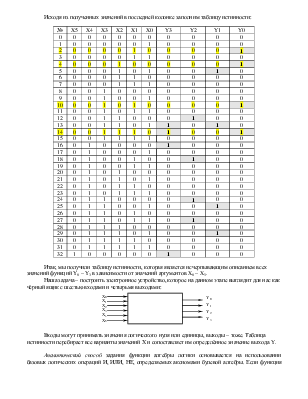
Исходя из полученных значений в последней колонке заполним таблицу истинности:
|
№ |
X5 |
X4 |
X3 |
X2 |
X1 |
X0 |
Y3 |
Y2 |
Y1 |
Y0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
6 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
7 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
8 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
9 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
10 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
11 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
12 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
13 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
14 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
15 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
16 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
17 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
18 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
19 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
20 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
21 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
22 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
23 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
24 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
25 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
26 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
27 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
|
28 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
29 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
30 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
31 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
32 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Итак, мы получили таблицу истинности, которая является исчерпывающим описанием всех значений функций Y0 – Y3 в зависимости от значений аргументов X0 – X5.
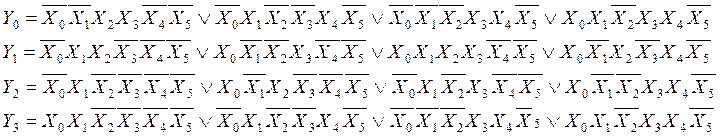
Упростим ФАЛ методом карт Карно:
![]()
|
X3X4X5 X0X1X2 |
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
|
000 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
001 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
011 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
010 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
110 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
111 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
101 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Карта Карно не содержит смежных клеток => в Y0 нет сливающихся конституент.
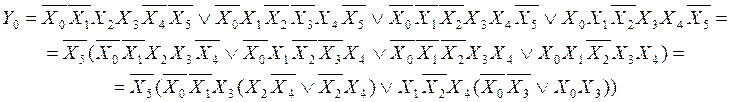
Теперь разберём Y1:
![]()
Карта Карно:
|
X3X4X5 X0X1X2 |
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
|
000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
001 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
011 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
010 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
110 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
111 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
101 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
100 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
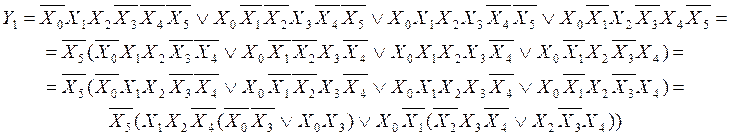
Теперь разберём Y2:
![]()
Карта Карно:
|
X3X4X5 X0X1X2 |
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
|
000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
001 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
011 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
010 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
110 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
111 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
101 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
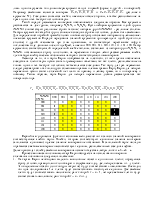
Есть смежные клетки. Несмотря на то, что они расположены далеко друг от друга, примем во внимание тот факт, что карта Карно является замкнутой, то есть клетки, расположенные на противоположных сторонах карты также являются смежными. Первая и третья конституенты сливаются по переменной X3 в сосиську:
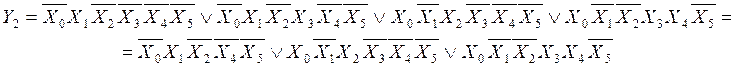
Минимальная СДНФ:
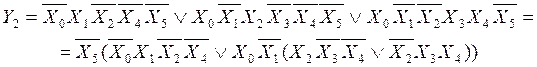
И, наконец, Y3:
![]()
Карта Карно:
|
X3X4X5 X0X1X2 |
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
|
000 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
001 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
011 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
010 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
110 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
111 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
101 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
100 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Соседних клеток нет, контуров нет, склеивания нет. СДНФ является тупиковой.
Минимальная СДНФ:
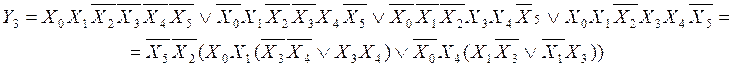
Итак, мы получили минимизированную систему 4-х уравнений:
![]()
![]()
![]()
![]()
В нашем распоряжении следующие двухвходовые элементы серии К1533:
|
1533ЛА3 |
Четыре 2И-НЕ |
|
1533ЛА8 |
Четыре 2И-НЕ с открытым коллектором (элементы контроля) |
|
1533ЛА9 |
Четыре 2И-НЕ с открытым коллектором |
|
1533ЛА12 |
Четыре буферных 2И-НЕ с высокой нагрузочной способностью |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.