Исследование пассивных резистивных четырёхполюсников (Лабораторная работа № 8)

Лабораторная работа № 8

Исследование пассивных резистивных четырёхполюсников.

Цель работы: Изучение основных характеристик и уравнений пассивных четырёхполюсников.

Задача работы: Экспериментальное определение некоторых параметров несимметричных четырёхполюсников и параметров каскадно или параллельно соединённых четырёхполюсников.

Используемые приборы: Стенд лабораторной работы №8.

Основные понятия и законы:

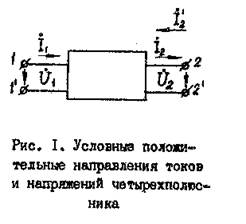Часть электрической цепи, рассматриваемая по отношению к любым двум парам ее выводов, называется четырехполюсником.

Вывода четырёхполюсника, к которым присоединяется источник электрической энергии, называются входными или входом, а выводы, к которым присоединяется нагрузка, - выходными или выходом. Пассивные четырехполюсники не содержат источников электрической энергии. Четырёхполюсник является симметричным, если перемена местами его входных и выходных выводов не изменяет токов и напряжений в цепи, с которой он соединен.

Если для четырехполюсника выполняется теорема обратимости, то такой четырехполюсник называется обратимым, т.е. передаточные сопротивления входного и выходного контуров одинаковы. Симметричные четырехполюсники всегда обратимы. Пассивные линейные четырехполюсники также являются обратимыми.

Для четырехполюсника, изображенного на рис. 1, можно записать следующие уравнения:

через Y - параметры, форма

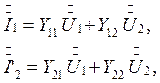                                                                                                                                                                  (1)

через Z - параметры, форма

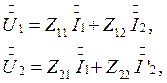                                                                                                                                                                   (2)

черер А - параметры, форма

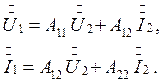                                                                                                                                                                  (3)

Коэффициенты каждой системы уравнений четырехполюсника могут быть выражены через коэффициенты любой другой системы (см. табл. 1 и 2). Для обратимых четырехполюсников справедливы соотношения

                                                                                 .

Коэффициенты Y в уравнениях (1) представляют собой входные и передаточные проводимости для входного и выходного контуров:

Y₁₁ - входная проводимость со стороны выводов 1 при закороченных выводах 2;

Y₂₂ - входная проводимость со стороны выводов 2 при закороченных выводах I;

Y₂₁ - передаточная проводимость при закороченных выводах 2;

Y₂₁ - передаточная проводимость при закороченных выводах 1.

Для симметричного четырехполюсника выполняется условие

                                                                                 .

Коэффициенты  в уравнениях (2) представляют собой входные и передаточные сопротивления при холостом ходе на соответствующих выводах.

Таблица 1

Определители, выраженные через коэффициенты четырёхполюсника

Для симметричного четырехполюсника выполняется условие

                                                                                 .

Форма  применяется обычно для анализа условий передачи электрической энергии от входных выводов к выходным, причем четырехполюсник» включенный между источником и приемником, может состоять из нескольких четырехполюсников, соединенных каскадно. Для симметричного четырехполюсника выполняется условие

                                                                                 .

Для экспериментального определения параметров четырехполюсника необходимо провести опыты, при которых ток или напряжение в правых частях уравнений (1), (2), (3) обращаются в нуль.

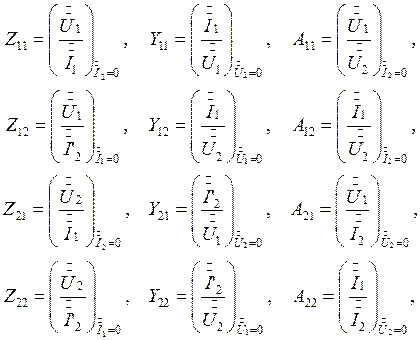
В общем случае для синусоидальных токов и напряжений все коэффициенты – величины комплексные. Характеристическими называются сопротивления и , удовлетворяющие следующему условию: входное сопротивление  со стороны выводов 1 четырехполюсника, нагруженного сопротивлением , равно ; входное сопротивление  со стороны выводов 2 четырехполюсника, нагруженного сопротивлением , равно . Условие, когда четырехполюсник нагружен соответствующим характеристическим сопротивлением, называется условием согласованной нагрузки или согласованного включения.

Характеристические сопротивления могут быть определены через А-параметры:

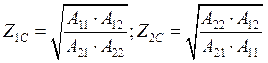
или через Z и Y-параметры

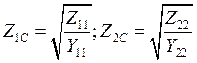
Дня четырехполюсников могут быть построены различные схемы замещения. На рис. 2 показаны две схемы замещения Т- и П-образные. Схемы замещения облегчают исследование свойств рассматриваемой цепи.

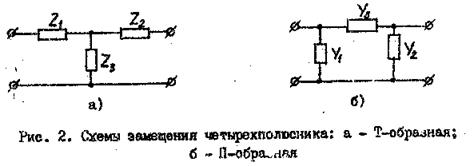
Параметры элементов схем замещения, можно определить по следующим формулам

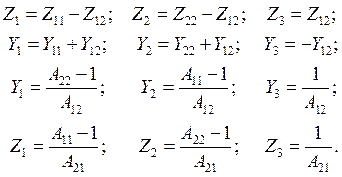
Пассивный П-обравный четырехполюсник может быть преобразован