Разработка метода поиска повреждения контактной сети с использованием наведенного напряжения, страница 2

ЭЛЕКТРИЧЕСКОЕ ВЛИЯНИЕ

Заменяя систему контактных сетей эквивалентной однопроводной цепью, удобно для количественной оценки электрического влияния воспользоваться схемой емкостной и гальванической связи между влияющей, подверженной влиянию цепями и землей, показанной на рис. 2.1.

                        i                                                              

                        A                                                            

                   z                        

                    O

Рис 2.1. Схема, поясняющая электрическую связь между влияющей и подверженной влиянию однопроводными воздушными линиями

Здесь i― эквивалентная влияющая цепь, к которой подведено фиксированное

Напряжение  от внешнего источника тока; А― подверженная влиянию однородная воздушная цепь с распределенными постоянными, замкнутая на сопротивление z.

       Для двух последовательно соединенных электрических цепей i―A и А―О, у которых можно пренебречь активными составляющими полных проводимостей утечки ( и , а также потерей напряжения в цепи А, вызываемой емкостным током, уравнение электрической связи запишем так:

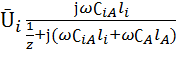= ,                       (2.9)

где ―индуктированное напряжение в подверженной влиянию однопроводной цепи А, в;  погонная эквивалентная взаимная емкость между однопроводными цепями i и А( коэффициент емкостной связи), равная взаимной емкости между системой контактных подвесок и цепью А,ф/км;  емкость провода А по отношению к земле, ф/км; ― длина параллельного сближения между однопроводными цепями I и А,км; ― длина подверженной влиянию однопроводной цепи, км; Z― cопротивление, на которое замкнута однопроводная цепь А, ом; ω― круговая частота влияющего тока,.

Для изолированной от земли, у которой сопротивление Z=, уравнение (2.9)

примет вид

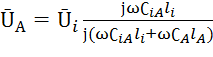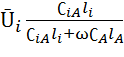                   =                      (2.10)

На электрических железных дорогах переменного тока электроснабжение линейных нетяговых потребителей во многих случаях осуществляется от продольных линий электропередачи по системе ДПР, провода которых обычно подвешивают на опорах контактной сети с одной стороны путей на станциях и с противоположных сторон путей на перегонах. Являясь линиями несимметричными, они так же, как и контактные подвески, оказывают электрическое влияние на воздушные линии. Фаза одного из проводов линии ДПР совпадает с фазой контактной сети, а другого сдвинута на 12 Система

линейных уравнений Максвелла с учетом влияния проводов линии ДПР может быть записана

                              [(n+)];

                                                                                               (2.11)

                              () ,               

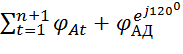где  ― среднее арифметическое значение взаимных потенциальных коэффициентов между контактными проводами, несущими тросами и проводами линии ДПР; ― средне арифметическое значение собственных потенциальных коэффициентов контактных проводов, несущих тросов и проводов линии ДПР; ― взаимный потенциальный коэффициент между влияющей цепью (контактным проводом, несущим тросом и проводом линии  ДПР, фаза которого совпадает с фазой контактной сети) и подверженным влиянию проводом; ― взаимный потенциальный коэффициент между проводом линии ДПР (у которого фаза сдвинута относительно фазы контактной сети на 12) и подверженным влиянию проводом; n― число несущих проводов и несущих тросов.

Решив систему уравнений (2.11), получим

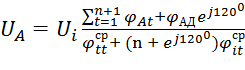                                .                    (2.12)

Таким образом оценивая влияние контактного провода соседнего пути, проводов линии ДПР на отключенный участок контактной сети приходим к выводу использования наведенного напряжения для определения наличия или  отсутствия короткого замыкания на отключенном участке контактной сети.

Метод основывается на применении трансформатора напряжения типа ЗНОМ-35 для измерения наведенного напряжения на отключенном участке контактной сети, анализа полученного сигнала и быстрого принятия мер по обнаружению места повреждения.