94. Молярная теплоёмкость твёрдого тела
по теории Эйнштейна описывается формулой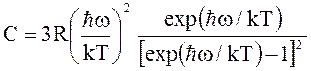 
.
Эта формула переходит в формулу закона Дюлонга и Пти при приближении
1)
= kT
2)
>> kT
3)
<< kT
4) = RT
95. Характеристическую температуру Дебая можно определить из выражения
1) 
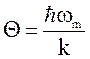
2) 
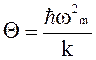
3) 
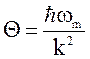
4) 
(
-
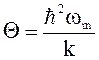
перечеркнутая постоянная Планка, k - постоянная Больцмана, 
m
- максимальная частота колебаний осцилляторов)
96. Графику зависимости молярной теплоёмкости твёрдого тела от температуры соответствует рисунок
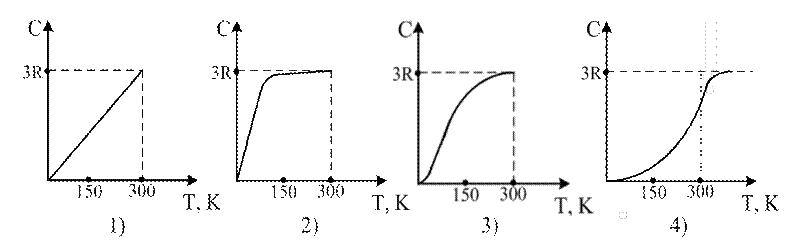
97. Сближение атомов при образовании кристалла вызывает
1) уменьшение ширины и увеличение высоты потенциального барьера для валентных электронов
2) увеличение ширины и увеличение высоты потенциального барьера для валентных электронов
3) увеличение высоты и уменьшение высоты потенциального барьера для валентных электронов
4) уменьшение ширины и уменьшение высоты потенциального барьера для валентных электронов
98. В кристалле валентные электроны принадлежат одному конкретному атому в течение
1) 10-12 с
2) 10-13 с
3) 10-8 с
4) 10-15 с
99. При объединении отдельных атомов в кристалл ширина энергетического уровня
1) увеличивается в 107раз
2) увеличивается в 102 раз
3) уменьшается в 107 раз
3) увеличивается в 10-7 раз
100.Ширина энергетической зоны в кристалле зависит
1) от температуры кристалла
2) от температуры и расстояния между атомами
3) от расстояния между атомами
4) от заполнения зоны электронами
101. Сравните число электронов, которые могут находиться в 2s- и 2р-зонах кристалла натрия
1) Число электронов в 2р-зоне в 3 раза больше числа электронов в 2s-зоне.
2) Число электронов в 2р-зоне в 3 раза меньше числа электронов в 2s-зоне.
3) Число электронов в 2s-зоне в 3 раза больше числа электронов в 2р-зоне.
4) Число электронов в 2р-зоне равно числу электронов в 2s-зоне.
102.
Для атома натрия (
) валентные электроны находятся в
1) 1s - зоне
2) 2р - зоне
3) 2s - зоне
4) 3s - зоне
103. Не полностью заполненной электронами валентной зоной могут обладать
1) проводники
2) полупроводники
3) изоляторы
4) проводники и полупроводники
104. Если N - число частиц и G - число различных энергетических состояний, то специфика поведения квантовых частиц проявляется в случае
1) N<<G для фермионов и бозонов
2) N<<G для бозонов
3) N>>G для фермионов и бозонов
4) N>>G для фермионов
105. К бозонам относятся
1) электроны, фотоны
2) фотоны, фононы
3) электроны, фононы
4) протоны, нейтроны
106. Электронный газ в металлах - это
1) вырожденный коллектив частиц
2) невырожденный коллектив частиц
3) вырожденный коллектив частиц при температурах ниже температуры вырождения и становится невырожденным при температурах, больших температуры вырождения
4) невырожденный коллектив частиц при температурах ниже температуры вырождения и становится вырожденным при температурах, больших температуры вырождения
107. Полная статистическая функция распределения частиц по энегетическим состояниям N(E)dEописывается формулой
N(E)dE = f(E)×g(E)×dE,
в которой
1) f(E) - плотность энергетических состояний, приходящихся на интервал dE
2) g(E) - плотность энергетических состояний, приходящихся на интервал dE
3) f(E) - число частиц, имеющих энергию в интервале от Е до Е + dE
4) g(E) - число частиц в системе, имеющих энергию в интервале от Е до Е + dE
108. Плотность энергетических состояний можно рассчитать по формуле
1)
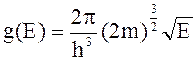
2) 
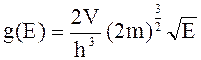
3) 
.
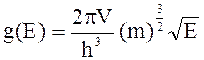4) 
.
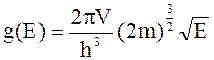109. Энергия Ферми зависит от концентрации электронов в кристалле согласно формуле
1)
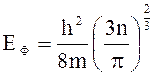
2) 
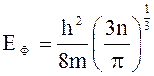
3) 
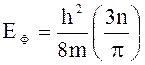
4) 
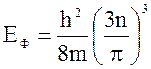
110. При температурах выше температуры абсолютного нуля (Т>0) вероятность заполнения электронами уровня Ферми равна
1) нулю
2) 0,5
3) единице
4) любому целому числу
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.