




ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ
Кафедра «Автоматика и телемеханика на железных дорогах»
Задание № 1
Разработка схем функционального контроля комбинированного дискретного устройства и оценка эффективности разработанных схем.
Работу выполнила: Работу проверил:
студентка гр. АС – 416 Кошелев А.П.
Цветкова М.А.
Санкт – Петербург
2007 г.
ВАРИАНТ 24.
Функциональная схема заданного комбинированного дискретного устройства представлена на рисунке 1.
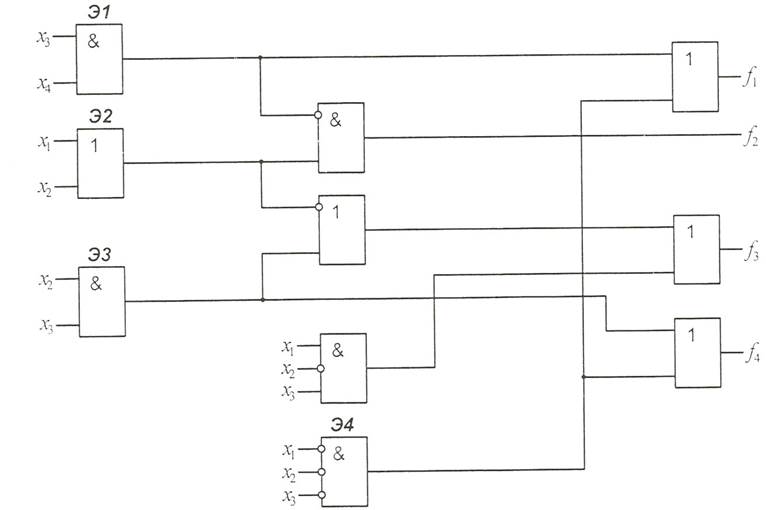
Рис.1.
1. Для заданного комбинированного дискретного устройства (КДУ):
1.1) Определяем сложность КДУ
L0 = 22
1.2) Определяем реализуемые КДУ булевы функции для каждого его выхода в исправном техническом состоянии
f1 = X3X4 v X1X2X3
f2 = X3X4 (X1 v X2)
f3 = ((X1 v X2) v X2X3)v X1X2X3
f4 = X2X3 v X1X2X3
1.3) Рассчитываем значения этих функций на всем множестве входных наборов заданного КДУ. Полученные результаты заносим в таблицу 1.
Таблица 1
|
n |
X1 |
X2 |
X3 |
X4 |
f1 |
f2 |
f3 |
f4 |
fp |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
4 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
5 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
6 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
7 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
|
8 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
9 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
10 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
11 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
|
12 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
13 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
14 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
15 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
2. Разрабатываем на базе заданного КДУ самопроверяемую дублированную систему с использованием схем сжатия (TRS). Рисунок 2.
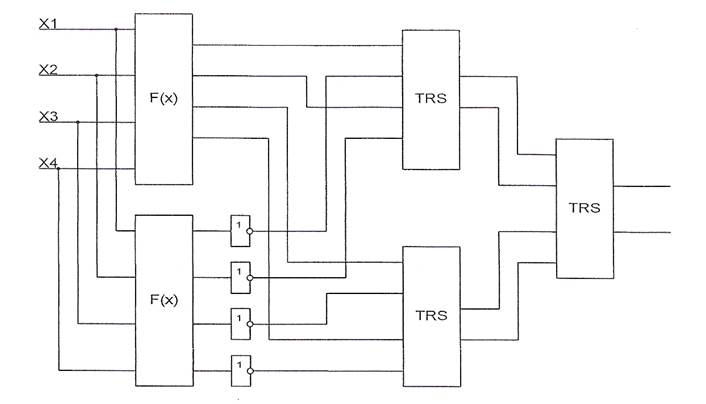
Рис.2
Определяем сложность самопроверяемой дублированной системы Lс учетом того, что LTRS = 12.
Lс = 2 . 22 + 4 + 3 . 12 = 84.
3. Для заданного КДУ разрабатываем самопроверяемую систему функционального контроля с использованием схемы контроля по паритету. Рисунок 3.
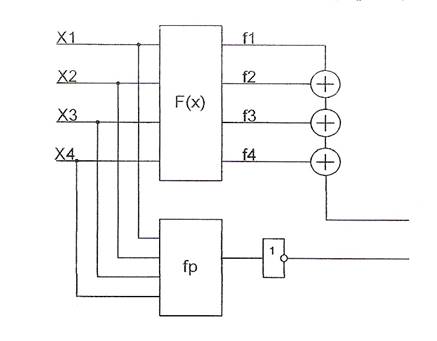
Рис.3
fp = f1 t f2 t f3 t f4
3.1) Определяем общую сложность заданного КДУ и дополнительных схем функционального контроля Lр.
|
1 |
1 |
1 |
1 |
|
|
1 |
1 |
1 |
|
1 |
1 |
||
|
|
1 |
1 |
|
fp = X2 V X2X3 V X1 X2X3X4
Функциональная схема контроля по паритету
![]()
![]()
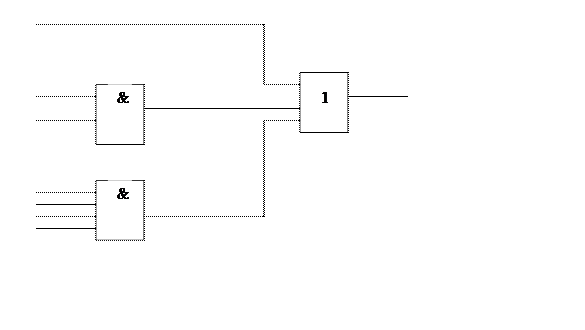
Рис.4
Lсп = 22 + 10 +3 . 6 + 1 = 51
3.2) Рассчитываем значение функции fр для каждого входного набора КДУ. Полученные значения заносим в таблицу 1.
4. Рассчитываем значения выходных функций при введении ошибок констант «0» и «1» в элементы Э1, Э2, Э3, Э4. Полученные значения заносим в таблицу 1.
Э1 const0 : f1 = X1X2X3 ; f2 = X1 v X2 ; f3 = ((X1 v X2) v X2X3)v X1X2X3 ; f4 = X2X3 v X1X2X3
Э1 const1 : f1 =1 ; f2 = 0 ; f3 = ((X1 v X2) v X2X3)v X1X2X3 ; f4 = X2X3 v X1X2X3
Э2 const0 : f1 = X3X4 v X1X2X3; f2 = 0 ; f3 = 1 ; f4 = X2X3 v X1X2X3
Э2 const1 : f1 = X3X4 v X1X2X3 ; f2 = X3X4 ; f3 = X2X3 v X1X2X3 ; f4 = X2X3 v X1X2X3
Э3 const0 : f1 = X3X4 v X1X2X3; f2 = X3X4 (X1vX2); f3 = (X1vX2) v X1X2X3; f4 = X1X2X3
Э3 const1 : f1 = X3X4 v X1X2X3 ; f2 = X3X4 (X1 v X2) ; f3 =1 ; f4 = 1
Э4 const0 : f1 = X3X4 ; f2 = X3X4 (X1 v X2) ; f3 = ((X1 v X2) v X2X3)v X1X2X3 ; f4 = X2X3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.