Построение схемы дублирования: Практическое задание № 1 по курсу "Основы технической диагностики"

Петербургский Университиет Путей Сообщения

Кафедра «Автоматика и телемеханика на железной дороге»

Практическое задание №1 по курсу ОТД.

Выполнил:

студент группы АТ-405

Тимур Атаханов

Санкт-Петербург

2007

Построение схемы дублирования

Для заданного КДУ определим реализуемые на его выходах функции алгебры-логики.

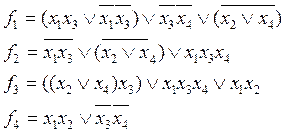
№	x1x2x3x4	f1f2f3f4	fp
0	0000	1101	1
1	0001	1100	0
2	0010	1100	0
3	0011	0100	1
4	0100	1101	1
5	0101	1100	0
6	0110	0100	1
7	0111	0110	0
8	1000	1101	1
9	1001	0100	1
10	1010	1000	1
11	1011	1010	0
12	1100	1111	0
13	1101	0111	1
14	1110	1011	1
15	1111	1011	1

Определим сложность КДУ L0. как число входов элементов (при этом инвертор на входе логического элемента не учитывается и считается, что инверсия входного сигнала выполняется внутри этого элемента)

L0=29

Разработаем на базе заданного КДУ самопроверяемую схему с использованием сжатия (TCR). Определим сложность системы Lg с учетом того, что Ltrc=12. В данном случае

Lg=2*29+4+3*12=98

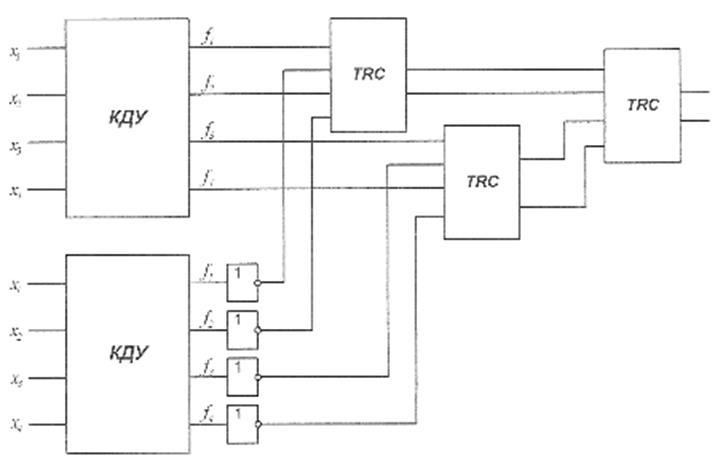
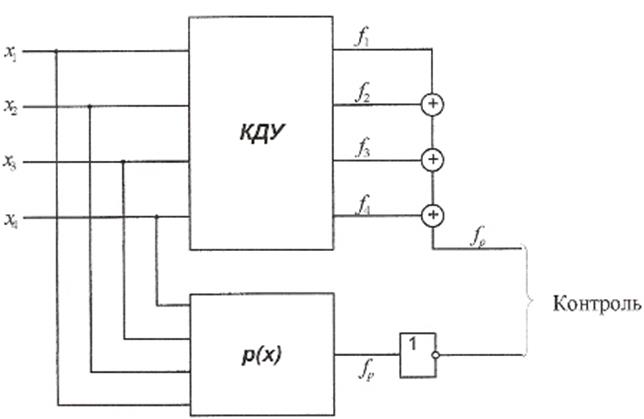
Построение схемы контроля методом паритета

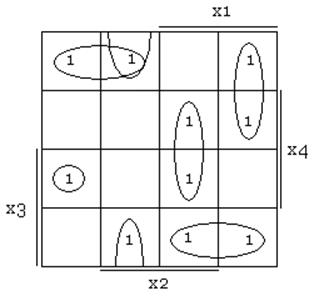
Построим дополнительный блок P(x), реализующий функцию паритета, и определим его сложность.

L(p)=25

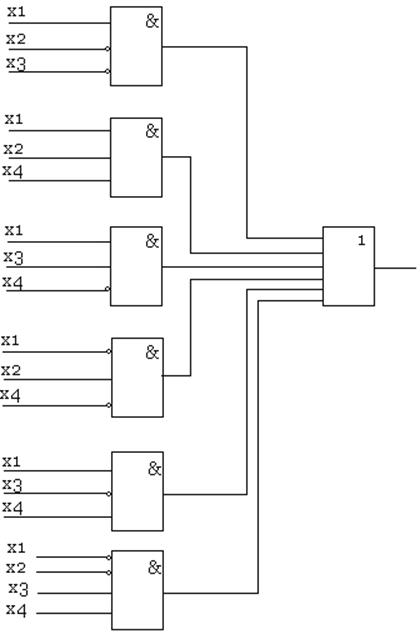
Разработаем самопроверяемую структуру контроля с использованием дополнительного блока P(x).  Определим сложность структуры Lpc с учетом того, что L(паритета)=6

Lpc=29+25+3*6+1=73

Анализ неисправностей КДУ.

Введем и пронумеруем неисправности “константа 1” (n1,n3,n5) и “константа 0” (n2,n4,n6) на выходах заданных элементов.

Для неисправности n1:

f¹₁= 1

f¹₂=

f¹₃=

f¹₄=

Для неисправности n2:

f²₁=

f²₂= 1

f²₃=

f²₄=

Для неисправности n3:

f³₁=

f³₂=

f³₃=

f³₄=

Для неисправности n4:

f⁴₁= 1

f⁴₂= 1

f⁴₃=

f⁴₄=

Для неисправности n5:

f⁵₁= 1

f⁵₂=

f⁵₃=

f⁵₄= 1

Для неисправности n6:

f⁶₁=

f⁶₂=

f⁶₃=

f⁶₄=

№	x1x2x3x4	f1f2f3f4	fp	f1f2f3f4 n1	fp1	f1f2f3f4 n2	fp2
0	0000	1101	1	1101	1	1101	1
1	0001	1100	0	1000	1	1100	0
2	0010	1100	0	1100	0	1100	0
3	0011	0100	1	1010	0	0110	0
4	0100	1101	1	1001	0	1101	1
5	0101	1100	0	1000	1	1100	0
6	0110	0100	1	1010	0	0110	0
7	0111	0110	0	1010	0	0110	0
8	1000	1101	1	1101	1	1101	1
9	1001	0100	1	1000	1	0100	1
10	1010	1000	1	1100	0	1100	0
11	1011	1010	0	1110	1	0110	0
12	1100	1111	0	1011	1	1111	0
13	1101	0111	1	1011	1	0111	1
14	1110	1011	1	1011	1	0111	1
15	1111	1011	1	1111	0	0111	1