Способ вращения. Угол между прямой и плоскостью

Вопрос №15

Способ определения угла наклона плоскости общего положения к плоскостям проекций H и V.

                              Ответ:

Способ вращения:

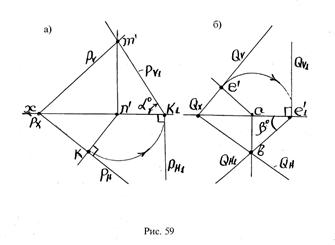
Заданы плоскости Р и Q следами. Требуется определить угол наклона плоскости Р к плоскости Н и плоскости Q к плоскости V (рис. 59).

Решение: Определяется натуральная величина угла , составленного плоскостями Р и Н:

Выбирается ось вращения m’n’, перпендикулярная плоскости  Н и расположенная в плоскости V (см.рис.59,а).

Из точки n’ опускается перпендикуляр на след Рн. Точка К – основание перпендикуляра.

След Рн поворачивается вокруг точки    Õ n’ до положения, когда между осью Х и следом образуется угол 90° (точка К₁).

Точка m’ расположена на следе Рv. Очевидно, при вращении  плоскости Р вокруг оси m’n’ точка m’ будет неподвижной. Она и определит положение следа Рv₁  совместно с точкой К₁   (Рх).

В результате выполненных преобразований получили фронтально – проектирующую плоскость Р₁. Угол образованный следом Рv₁  и осью Х представляет натуральную величину угла наклона плоскости Р к плоскости Н (угол a° , см.рис.59,а).

Определяется угол, образованный плоскостями Q и  V. Ось вращения плоскости располагается в плоскости Н перпендикулярно плоскости V (ось ab – см.рис.59,б).

След  Qv  поворачивается вокруг точки  а  до положения, когда между следом и осью Х образуется угол  90°. В результате получают новое положение следа  - Q_v1.

След  Q_H1  определяется положением неподвижной точки “в” расположенной на следе Qн и точкой С₁.

Из рис.59,б видно, что после преобразования плоскость  Q  стала горизонтально – проектирующей плоскостью. Угол, образованный следом Q_H1  и осью Х является натуральной величиной угла наклона плоскости Q к плоскости V.

Вопрос №18

Способ определения угла между прямой и плоскостью ( прямая и плоскость - общего положения).

                                   Ответ:

Угол между прямой и плоскостью:

Угол между прямой и плоскостью называется острый угол, образованный этой прямой и ее проекцией на данную плоскость (рис.44,а).

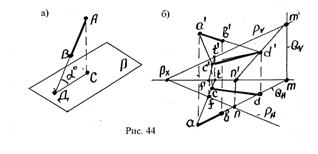
Заданы проекции прямой АВ и следы плоскости Р. Требуется определить угол между прямой и плоскостью (рис.44,б).

Решение: Определяется точка пересечения прямой АВ с плоскостью Р: через проекцию ab проводится горизонтально – проектирующая плоскость Q и находится  линия пересечения плоскостей Р и Q  (линия МN, см.рис. 44,б). Затем  определяется точка пересечения линий МN и АВ – точка D.

Из точки А опускается перпендикуляр на плоскость Р. С помощью вспомогательной горизонтально – проектирующей плоскости находится точка пересечения перпендикуляра с линией пересечения плоскостей S и Р (точка С, см.рис.44,б). На горизонтальной и фронтальной проекциях через точки D и С проводятся  прямые.

В результате построения получают проекции угол АВС.