Возможно доклад, который я сейчас хочу представить вашему вниманию, покажется несерьезным и даже шутливым, на фоне остальных докладов конференции, но это первое впечатление, которое, думаю, впоследствии измениться.
Давайте рассмотрим действие
сосредоточенной силы Р на упругую консольную балку, когда точка приложения силы
движется вдоль балки по заданному закону ξ=ξ(t).
Представляется очевидным, что при достаточно малых скоростях движения нагрузки
![]() (t) мы можем считать ускорения
также достаточно малыми, поэтому можем пренебречь инерционными эффектами и
усилиями в системе в любой момент времени и определять усилия из уравнений
равновесия. То есть мы можем перейти к квазистатическому решению. То есть для
любого положения линии действия силы Р, все элементы изгиба можно определять
путем статического решения, выполняемого обычными методами сопромата.
(t) мы можем считать ускорения
также достаточно малыми, поэтому можем пренебречь инерционными эффектами и
усилиями в системе в любой момент времени и определять усилия из уравнений
равновесия. То есть мы можем перейти к квазистатическому решению. То есть для
любого положения линии действия силы Р, все элементы изгиба можно определять
путем статического решения, выполняемого обычными методами сопромата.
Найдем потенциальную энергию деформации нашей балки, когда точка приложения силы совпадает с концом балки, т.е. ξ=l , а f – статический прогиб правого конца балки. Думаю, что любой в этой аудитории ответит, что потенциальная энергия деформации будет равна половине произведения силы Р на прогиб f . Эта потенциальная энергия накоплена в результате работы, которую совершает сила Р при постепенном опускании точки ее приложения на величину f . Если мы вычислим работу силы Р, как произведение Р f , то получим результат вдвое больший потенциальной энергии деформации. Возникает вполне логичный вопрос, а куда израсходовалась вторая половина работы?
Возможно, было неправильным считать, что мы можем перейти к квазистатическому представлению задачи для случая подвижной нагрузки, и что при любой, сколь угодно малой скорости движения нагрузки необходимо учитывать инерционные свойства системы и (или) вязкость материала. Тогда мы могли бы ожидать, что вторая половина работы силы Р переходит в кинетическую энергию балки и постепенно рассеивается.
Рассмотрим еще одну классическую задачу сопромата, из разряда тех, что нам известны еще со школьного курса физики.
Система представляет собой прямолинейный стержень, нагруженный растягивающей силой Р, точка приложения которой движется вдоль оси стержня по некоторому заданному закону ξ(t). Пусть l- длина стержня и Δ l – его удлинение в момент, когда точка приложения силы достигает конца стержня. Итак, потенциальная энергия растяжения будет (РΔ l/2). А работа, совершенная к этому моменту силой Р будет находиться по выражению: Р(l+ Δ l), или, принимая во внимание малость деформации Δ l, можем записать как Рl. Тут уже результат отличия работы и потенциальной энергии будет различаться не в 2 раза, а в тысячи.
Возможно, и в самом деле квазистатическая трактовка задачи таких задач содержит коренную ошибку и принципиально недопустима?
Чтоб исключить какие бы то ни было двусмысленности предлагаю отвлечься от приведенных схем и рассмотреть общий случай переменной нагрузки:
p=p(x,t) (1) любым образом меняющейся во времени и произвольно распределенной вдоль оси произвольно закрепленной балки.
Определим элементарную работу
нагрузки (1) за время dt. Обозначим прогиб w=w(x,t) (2).
Тогда выражение вертикальной скорости любого сечения балки будет в виде ![]() . А элементарное перемещение соответственно
будет (
. А элементарное перемещение соответственно
будет (![]() )dt. И тогда элементарная работа
определиться выражением:
)dt. И тогда элементарная работа
определиться выражением:
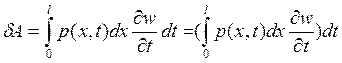 (3)
(3)
Для того, чтоб с помощью (3) найти элементарную работу «движущейся» сосредоточенной силы Р, представим ее в виде нагрузки p(x,t), которая задана следующим образом:
Здесь ε – длина малого отрезка, на котором нагрузка отлична от нуля, Р – равнодействующая нагрузки. При этом координата ξ некоторым образом зависит от времени.
Теперь мы можем записать:
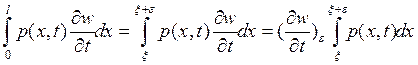 ,
где
,
где 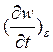 - среднее
значение вертикальной скорости балки на отрезке ε. Входящий сюда интеграл равен
Р, так что можем записать :
- среднее
значение вертикальной скорости балки на отрезке ε. Входящий сюда интеграл равен
Р, так что можем записать :
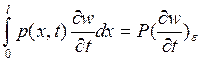 (4)
(4)
Для того чтобы перейти к
случаю действия сосредоточенной силы Р, необходимо устремить длину ε к 0,
подставить в (4) вместо 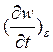 вертикальную скорость течения х=ξ, равную
вертикальную скорость течения х=ξ, равную 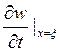 . Тогда
выражение для элементарной работы (3) примет вид:
. Тогда
выражение для элементарной работы (3) примет вид:
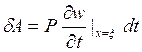 (5),
но произведение
(5),
но произведение 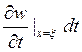 это элементарное перемещение сечения балки, расположенного под силой.
Тогда мы получаем, что элементарная работа силы Р оказывается равной
произведению этой балки на элементарное перемещение сечения балки, а не
геометрической точки приложения силы!
это элементарное перемещение сечения балки, расположенного под силой.
Тогда мы получаем, что элементарная работа силы Р оказывается равной
произведению этой балки на элементарное перемещение сечения балки, а не
геометрической точки приложения силы!
На рисунке мы можем видеть
разницу между элементарным вертикальным перемещением сечения балки 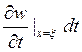 и
элементарным вертикальным перемещением начала вектора силы Р.
и
элементарным вертикальным перемещением начала вектора силы Р.
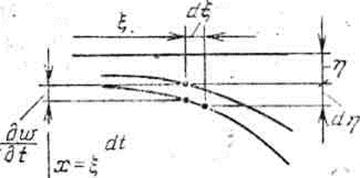
Которое представляет собой полный дифференциал функции w(x,t) в точке х=ξ.
Обычно в курсах механики чаще всего можно встретить такое определение элементарной работы:
«Элементарная работа силы равна скалярному произведению силы на элементарное перемещение».
Иногда можно встретить и более подробное описание, как например в курсе П. Аппеля : «…при вычислении элементарной работы силы... как возможной, так и действительной, не следует смешивать материальную точку, к которой приложена сила, с геометрической точкой ее приложения. В выражениях элементарной работы F* ММ1' cos(F, MM'), Fvcos(F, v) символы ММ' и vобозначают бесконечно малое перемещение и скорость той материальной точки, к которой приложена сила, а не перемещение и скорость геометрической точки приложения силы». Конечно, во многих случаях (и даже весьма часто, можно сказать, обычно) названные точки совпадают и цитированное уточнение становиться излишним, но в рассматриваемых нами задачах о действии подвижной нагрузки оно необходимо.
Вернемся к нашей задачи. Из сопромата нам известны выражения для прогиба:
Вертикальная скорость произвольного сечения балки
Под силой, т.е. при х=ξ, имеем 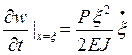 (10)
(10)
Отмечу, что, так как 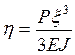 ,
вертикальная скорость геометрической точки приложения силы определяется
выражением:
,
вертикальная скорость геометрической точки приложения силы определяется
выражением:
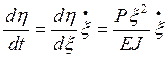 (11) , а
это ровно в два раза больше вертикальной скорости сечения!
(11) , а
это ровно в два раза больше вертикальной скорости сечения!
Теперь, согласно (5) и (10) элементарная работа силы Р определяется в виде:
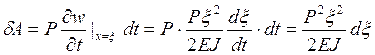
Интегрируя по всей длине балки, находим работу, совершенную силой Р к моменту времени, когда сила достигнет конца балки:
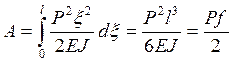
То есть мы получили результат, который точно равен потенциальной энергии изгиба в тот же момент. Вывод: вычисление работы по выражению Pf ошибочно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.