Электронно-оптическая система

ГЛАВА 4

ЭЛЕКТРОННО-ОПТИЧЕСКАЯ СИСТЕМА

С 1968 года [4] на предприятии «Светлана-Электронприбор» используются многолучевые электронно-оптические системы (Рис.21).

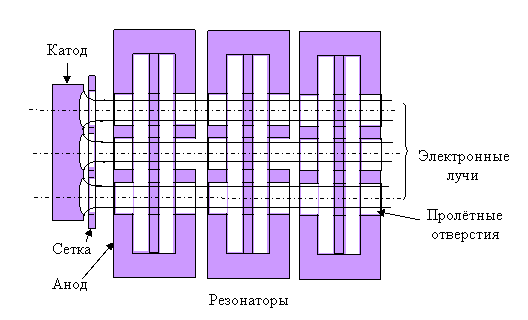
Рис.21 Схема многолучевого клистрона

Они представляют собой систему из катода с сеткой (маской) и высокочастотной структуры с несколькими каналами. Отношение размера катода и размера луча в канале (сходимость электронного луча) небольшое. Чем больше лучей при заданном общем токе электронного потока, тем меньше первеанс каждого луча и меньше нежелательное влияние пространственного заряда (плотность пространственного заряда пропорциональна первеансу луча I/U^3/2). Число лучей ограничено технологическими трудностями изготовления, особенно в коротковолновых диапазонах. Но они успешно преодолеваются. Многолучевые системы позволили существенно снизить сопротивление электронного потока и увеличить общий первеанс усилителей в 7-40 раз по сравнению с однолучевым потоком. Это достигается увеличением площади катода и плотности тока с эмиттирующей поверхности с соответствующим сокращением срока службы.

Для расчёта статического электронного луча от катода до коллектора используется программа «Antra» (Г.П.Зыбин, 1979, ЛЭТИ).

Программа «Antra» предназначена для решения двухмерных задач в декартовой или цилиндрической системах координат. Она позволяет рассчитывать свойства  потоков заряженных частиц в статических электрическом и магнитном полях с учетом пространственного заряда

Программа позволяет по заданным потенциалам, геометрии электродов и осевому распределению магнитного поля вычислять электростатическое и магнитное поля в системе, траектории заряженных частиц на всей длине прибора от катода до коллектора, параметры потока частиц – первеанс, распределение плотности тока луча, скоростей частиц и объемной плотности заряда по сечению пучка.

В основу программы положен итерационный метод решения систем уравнения, описывающих интенсивные потоки заряженных частиц. Эта система состоит из уравнения Пуассона, определяющего электростатическое поле с учетом пространственного заряда, уравнение движения заряженной частицы в электрическом и магнитном полях и уравнения непрерывности для отдельной трубки тока.

Уравнение Пуассона решается методом конечных разностей на неравномерной сетке с кусочно-постоянным шагом в замкнутой области, на границах которой заданы условия Дирихле или Неймана. Расчеты проводятся методом последовательной верхней релаксации.

Компоненты градиента электростатического поля в произвольной точке, необходимые для расчета траекторий, определяются по значениям потенциалов в узлах сетки, найденных в результате численного решения уравнений Пуассона.

Для вычисления компонент  вектора магнитной индукции во внеосевых точках используются формулы аналитического продолжения по известным значениям индукции на оси симметрии.

Возможно включение в расчёт неоднородного магнитного поля.

Целесообразен расчёт траекторий отдельными кусками луча с передачей данных от одного куска  к другому. В результате для заданной геометрии получается форма траекторий по всей длине канала, ток луча, первеанс луча (I/U^3/2), распределение плотности тока по сечению луча.

Такие графики представлены на рис 27-29 при разных величинах внешнего магнитного поля. Графики созданы для нескольких величин внешних полей. Внешнее магнитное поле отсутствуют (рис 27) магнитное поле, рассчитанное на теоретический минимум (рис 28) и магнитное поле с величиной магнитной индукции больше теоретического минимума (рис 29). Далее способ реализации этого поля будет описан в главе 5 – расчет магнитной системы.

Точность расчёта по программе «Antra» неоднократно проверялась и несоответствий эксперименту по первеансу не наблюдалось. Что касается несоответствий эксперименту по токопрохождению, то они объясняются несовершенством сборки пушки и несовершенством магнитной системы.