Акустический метод. Элементы теории упругих волн в геологической среде

Акустический метод (АМ)

Элементы  теории упругих волн в геологической среде

Под воздействием  силы  в  источнике в геологической   среде   возникают  и  распространяются  напряжения  (упругие силы)   и  упругие  деформации.  Пусть  на единичный   элемент  среды    (dxdy)

действует   сила    с  нормальной   и тангенциальной      составляющими – напряжениями .   Под  их   воздействием единичный          элемент        сжимается 

(на    линейную   величину       )      и

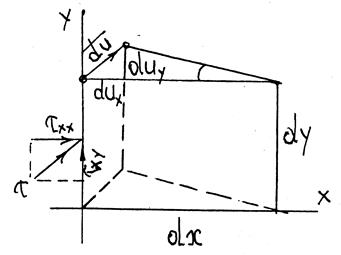скашивается (на  угловую величину    )  Относительные    величины      и      называются  соответсвенно нормальной и тангенциальной деформациями, которые создают в среде продольные Р (сжатия - растяжения)  и  поперечные  S (сдвиговые) волны.

Распространение упругих волн в среде описывается волновым уравнением.

Выводится оно из фундаментального 2-го закона Ньютона

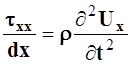, где   - элементарная сила,   - элементарная масса (плотность) , 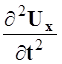 - ускорение смещения элемента среды.   По закону   Гука упругие  напряжения пропорциональны  деформациям:               

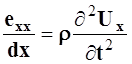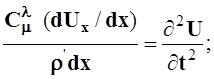
Делаем подстановки в уравнение :      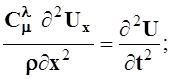  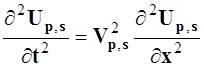;            (*)   [] , где

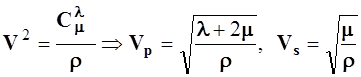
                  - скорости  продольной и поперечной волн, 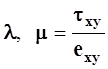      -  упругие  константы Ламэ                                                                                           

Волновое уравнение (*) показывает, что ускорение смещения во времени пропорционально ускорению смещения

..........................................................................................................................

Тот факт, что уравнение Ламэ  распадается на 2 независимых уравнения, свидетельствует, что продольная ( Р )и поперечная ( S ) волны распространяются независимо. Из формул для   и   следует, что скорость продольной волны  >= чем поперечной. Константы Ламэ  - важнейшие характеристики горных пород. Измерив скорости   и       и определив независимым путем плотность  , можно по вышеприведенным формулам рассчитать константы  и , a зная их – другие  упругие  модули горных пород:                                                                       

Модуль Юнга 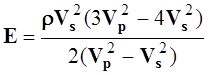                                     - плотность коэффициент Пуассона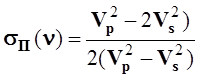                    

модуль сдвига                          

объемный модуль 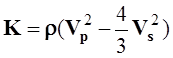                         всестороннего сжатия сжимаемость                          

Знание этих модулей необходимо для изучения прочностных свойств горных пород: коэффициент Пуассона обнаруживает связь с нефтеносностью коллектора.

Рассмотренная теория относится к однородным изотропным средам. Реальные горные породы являются многофазными  пористыми средами. В них возникают два типа продольных волн 1 и 2-го порядка. Одна из них - продольная  волна 1-го рода   - волна сжатия, аналогичная продольной волне в однофазной среде . Вторая – продольная 2-го рода – связана с фильтрацией флюида в порах породы под действием  акустического поля перепадов давления. На НЧ движения флюида в этой волне подчиняется, уравнению диффузии, поэтому и называют волной диффузионного типа. В АК она используется для выделения в разрезе проницаемых пластов – коллекторов .

Важнейшие параметры, влияющие на скорость и поглощение упругих волн – коэффициенты пористости и проницаемости (рис.        ).

Важнейшая особенность АМ – существенная зависимость показаний от        т и п а порового пространства. Трещины можно аппроксимировать эллипсоидами вращения. Если давление действует вдоль их малой оси, оболочка такой формы обладает меньшей жесткостью, чем сферическая.Между тем форма каверны близка к сферической(рис.      ) .Промежуточной жесткостью обладают поры гранулярного типа. Поэтому при   о д и н а к о в о й    пористости скорость в кавернозных породах должна быть больше, а в трещиноватых – меньше, чем в гранулярных.  Таким образом в АМ существуют предпосылки для оценки   т и п а   порового пространства.

Практический интерес представляет изучение зависимостей акустических характеристик пород от вида флюида – порозаполнителя: вода,    нефть или газ. Скорость продольных волн в водо- (ВП) ,  нефте- (НП) и газо-насыщенных (ГП)  породах – коллекторах отвечают условию      ; а поперечных  -                             

Снижение  при росте газосодержания связано с существенным увеличением сжимаемости флюида при появлении в нем газа. При большом насыщении газом    начинает увеличиваться за счет уменьшения плотности . Рост   при переходе от воды к нефти, а от нефти к газу обусловлен тем, что сдвиговая  жесткость породы   при этом не меняется, а плотность падает.

В большей степени влияние флюида – порозаполнителя сказывается на коэффицентах поглощения, для которых справедливы следующие неравенства:                   и