




Омский государственный технический университет
Кафедра ЭсПП(секция ПЭ)
«Расчёт магнитного поля двухпроводной линии»
Вариант 1-3-5
Выполнил: ст. гр. Э-323
Солопов Д.В.
Проверил: ассистент
Митяев А.Н.
Задание:
1. Определить индуктивность системы двух проводников, энергию магнитного поля, максимальные значения напряжённости, магнитной индукции и векторного потенциала.
2.
Рассчитать и построить зависимость
![]() и
и ![]() .
.
3.
Рассчитать ЭДС и ![]() прямоугольной рамки с числом витков W=100,
расположенной в плоскости двухпроводной линии, если по линии проходит ток,
изменяющийся по закону
прямоугольной рамки с числом витков W=100,
расположенной в плоскости двухпроводной линии, если по линии проходит ток,
изменяющийся по закону ![]() с частотой
с частотой ![]() и действующим значением, равным значению
постоянного тока.
и действующим значением, равным значению
постоянного тока.
Вариант задания:
|
N0 |
D, см |
rпр, см |
N0 |
l, м |
|
N0 |
I, А |
b, см |
C, см |
|
1 |
5 |
0,2 |
3 |
15 |
1 |
5 |
5 |
18 |
2,4 |
1.Внешнее потокосцепление:
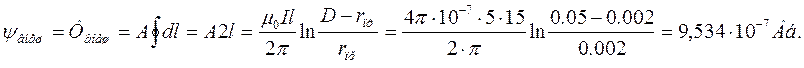
Внутреннее потокосцепление:
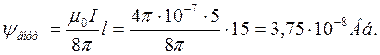
Индуктивность:
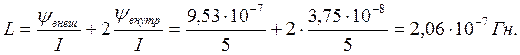
Зная индуктивность, легко найти энергию, которая сосредоточена в магнитном поле линии длиной l:
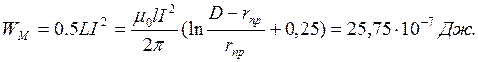
Значения ![]() ,
,![]() ,
,![]() :
:
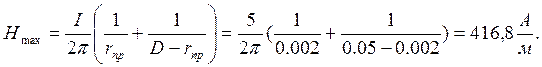
![]()
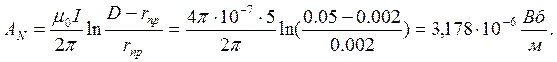
2.
Чтобы получить зависимость ![]() , сначала проводим
расчёт и построение кривой
, сначала проводим
расчёт и построение кривой![]() для левого провода, применяя формулу:
для левого провода, применяя формулу:
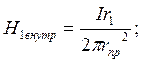 и
и 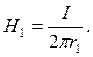 Расчёт сводим в таблице
1.
Расчёт сводим в таблице
1.
Таблица 1
|
r1, м. |
rпр=0,002м. |
0,02 |
0,03 |
0,04 |
D-rпр=0,048 |
D+rпр=0,052 |
0,06 |
0,07 |
|
H1, А/м |
398 |
39,8 |
26,5 |
19,9 |
16,5 |
15,2 |
13,2 |
11,3 |
Кривая ![]() , построенная по данным таблицы, изображена на рис.1.
Зависимрсть
, построенная по данным таблицы, изображена на рис.1.
Зависимрсть ![]() для
правого провода изображается графически также по данным таблицы, как показано
на рис.2. Результирующая
для
правого провода изображается графически также по данным таблицы, как показано
на рис.2. Результирующая ![]() находится суммированием
ординат первых двух кривых (рис.3).
находится суммированием
ординат первых двух кривых (рис.3).
Кривая распределения векторного потенциала
рассчитывается с использованием формул 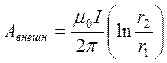 ,
, 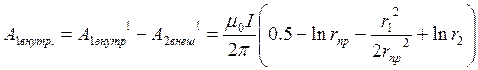 . При
этом следует учитывать, что расчёт по формуле
. При
этом следует учитывать, что расчёт по формуле 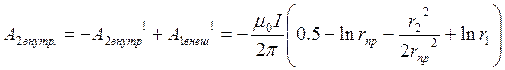 не обязателен , так как кривая
не обязателен , так как кривая ![]() может быть
получена по зависимости
может быть
получена по зависимости ![]() последовательным отображением сначала относительно оси
Z, а затем оси Y. Результаты
расчёта сведены в таблице 2.
последовательным отображением сначала относительно оси
Z, а затем оси Y. Результаты
расчёта сведены в таблице 2.
Таблица 2
|
r1, м |
0 |
0.001 |
r1=rпр= =0.002 |
0.02 |
0.03 |
0.04 |
D-rпр= 0.048 |
0.049 |
0.05 |
|
r2, м |
0.05 |
0.049 |
0.048 |
0.04 |
0.03 |
0.02 |
0.002 |
0.001 |
0 |
|
А1внут., Вб/м.. |
8.324 *10-6 |
4.52 *10-6 |
3.178 10-6 |
------- |
------- |
------- |
-------- |
-------- |
-------- |
|
А2внут., Вб/м. |
-------- |
-------- |
-------- |
------- |
------- |
------- |
-3.178 10-6 |
-4.52 10-6 |
-8.324 10-6 |
|
Авнеш., Вб/м. |
-------- |
-------- |
3.178 10-6 |
-0.69 10-6 |
0 |
0.69 10-6 |
-3.178 10-6 |
-------- |
-------- |
3.1. Расчёт ЭДС.
При расчёте ЭДС введём следующие допущения:
- полагаем катушку тонкостенной (n<<c, n=0), т.е. длина b и ширина c совпадают со средней линией катушки.
- Длина линии l>>b и, следовательно, конфигурация её поля не будет зависеть от координаты z.
ЭДС, наводимая в разомкнутой катушке, согласно закону ЭМИ:
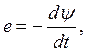
где: ![]() - потокосцепление,
обусловленное током i в линии и сцеплённое с витками катушки.
- потокосцепление,
обусловленное током i в линии и сцеплённое с витками катушки.
Т.к 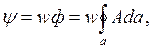
где: ![]() - средняя длина катушки.
- средняя длина катушки.
В силу симметрии расположения катушки значения векторного потенциала A слева и справа от плоскости y=0 одинаковы, поэтому расчёт A можно ограничить одной его половиной и записать:
![]()
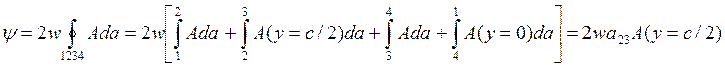
В выражении 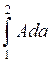 и
и 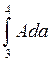 равны нулю, т.к. на участках 1-2 и 3-4 Ada=Adacos900.
равны нулю, т.к. на участках 1-2 и 3-4 Ada=Adacos900.
На участке 4-1 A(y=0)=0, т.к. r1=r2.
С учётом 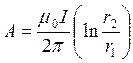 a23=b
последнее выражение будет иметь вид:
a23=b
последнее выражение будет иметь вид:
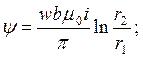
r1=D/2-C/2; r2=D/2+C/2
После подстановки получаем:
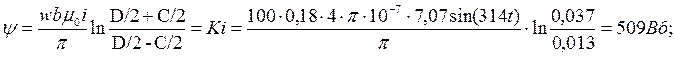
где 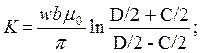
Используя предпоследнюю формулу, с учётом, что ![]() , рассчитываем ЭДС:
, рассчитываем ЭДС:
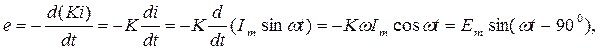
где: ![]() -
амплитудное значение ЭДС.
-
амплитудное значение ЭДС.
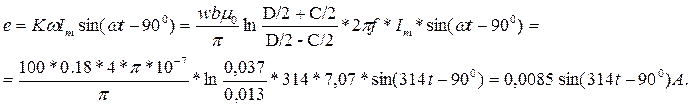
3.2. Расчёт тока короткого замыкания.
При расчёте тока короткого замыкания iк.з. будем полагать активное сопротивление катушки равным
нулю(Ra=0). На основании принципа неизменности
потокосцепления, согласно которому ток в катушке iк.з. будет вызывать магнитный поток(потокосцепление ![]() ) точно такой же величины, как и
поток(потокосцепление
) точно такой же величины, как и
поток(потокосцепление ![]() ), называемое током i,
протекающем в линии при разомкнутой катушке, можно записать:
), называемое током i,
протекающем в линии при разомкнутой катушке, можно записать:
![]() =
=![]() ,
,
где ![]()
Lk – индуктивность катушки, а ![]() определяется ранее.
определяется ранее.
Следовательно, ток iк.з. может быть рассчитан следующим образом: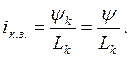
Индуктивность Lk для плоской прямоугольной катушки прямоугольного сечения может быть определена по формуле:
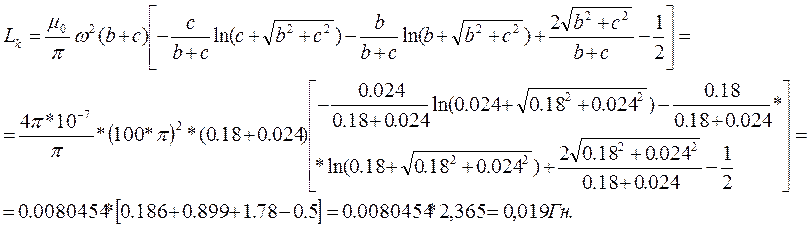
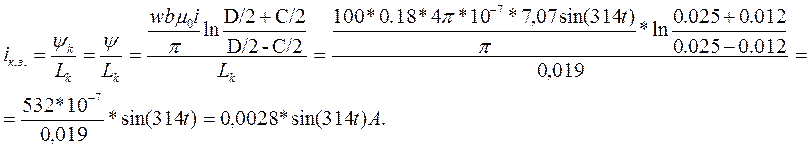
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.