Методы расчета установившихся режимов и основы проектирования электрических систем. Характеристики дальних электропередач и режимы их работы. Методы расчета и пути снижения потерь мощности и энергии в электрических сетях

сделать их применимыми для расчета на ЭВМ, их аппроксимируют в виде аналитических функций. Наиболее распространенной является параболическая аппроксимация:

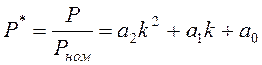,                                    (8.5)

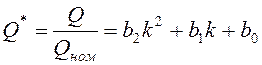,                                    (8.6)

где  – напряжение в относительных единицах; U_ном– номинальное напряжение; Р_ном и Q_ном – мощности, потребляемые при номинальном напряжении; a₁, a₂, a₀, b₁, b₂, b₀– коэффициенты аппроксимации, подчиняющиеся условиям , .

Число процентов, на которое изменяется мощность (активная или реактивная) при изменении напряжения на 1%, называется регулирующим эффектом нагрузки. Регулирующий эффект по активной мощности обозначим а_р,а по реактивной – b_р. Выразим их через коэффициенты аппроксимации.

,

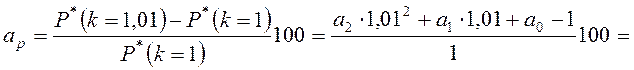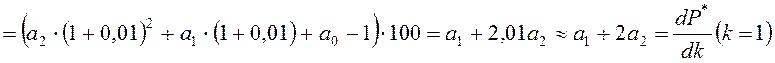, (8.7)

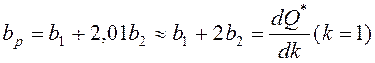.                           (8.8)

Для большинства электроприемников 0 ≤ а_р ≤ 2, 2 ≤ b_р ≤ 3.

Статистические характеристики являются самым общим и точным способом задания нагрузок. Недостаток: усложняются расчеты режимов электрических сетей и увеличивается количество исходных данных для этих расчетов.

8.2. Расчет разомкнутых питающих сетей по данным конца

Рассмотрим следующую электрическую сеть:

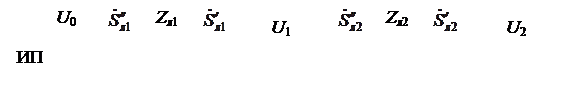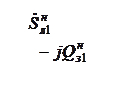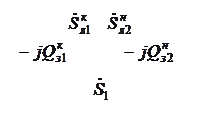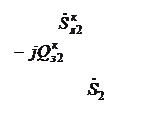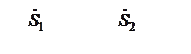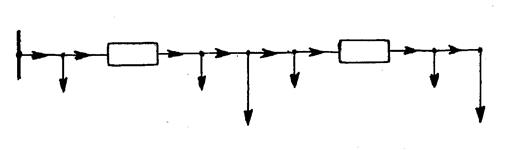
 Рис. 8.3. Схема рассматривае-

 мой сети:  ИП –  источник пи-          Рис. 8.4. Схема замещения сети (верхние индексы «н» и «к»

 тания; Л – воздушная линия              обозначают соответственно начало и конец линии)

Расчетом по данным конца называется расчет, который производится при известном напряжении в конце самого удаленного от источника питания участка сети. В данном случае известно напряжение U₂. Нагрузки заданы постоянной мощностью. Требуется определить мощности на всех участках сети и напряжения в узлах сети.

Расчеты режимов электрических сетей производятся обычно не в токах, а в мощностях. Для мощностей, как и для токов, выполняется первый закон Кирхгофа. Однако если ток на всех участках одной ветви одинаков, то мощность при переходе через сопротивление меняется на величину потерь мощности в этом сопротивлении.

Расчет производится в направлении от наиболее удаленного потребителя к источнику питания. Для схемы замещения, изображенной на рис. 8.4, порядок расчета будет следующим:

1. Определяется мощность в конце линии Л2

;

          2. Вычисляется зарядная мощность в конце этой же линии

;

          3. По первому закону Кирхгофа рассчитывается мощность :

;

4. Определяются потери мощности в сопротивлении Z_л2и мощность :

  ,

   ;

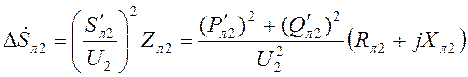5. Вычисляются продольная и поперечная составляющие падения напряжения в линии Л2:

,       ;

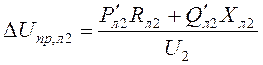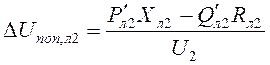6. Рассчитывается напряжение U₁:

;

7. Определяется зарядная мощность в начале линии Л2 и мощность :

,     ;

8. Вычисляется мощность в конце линии Л1

;

9. Производятся расчеты для линии Л1, аналогичные расчетам в линии Л2:

,    ,    ,    ,

,        ,

,   ,   .

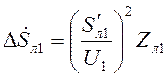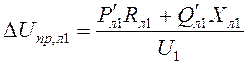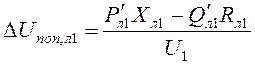          Расчет составляющих падения напряжения производится через мощность, протекающую по данной ветви со стороны известного напряжения. Если эта мощность направлена от искомого напряжения к известному, то при расчете искомого напряжения перед продольной составляющей падения напряжения ставится знак «плюс» (такая ситуация имеет место в рассмотренном примере). В противном случае перед продольной составляющей падения напряжения необходимо ставить знак «минус».

          В данном примере рассмотрена сеть с двумя линиями. Однако описанный метод может быть использован и для сети с произвольным количеством последовательных линий. Порядок расчета аналогичен.

          Уравнения установившегося режима электрической сети нелинейны