Проверка основного закона вращательного движения на маятнике Обербека (лабораторная работа), страница 2

                                                 .                                         (1)

Это уравнение относительно оси ОY запишется в виде:

                                                                                                    (2)

Из уравнения (2) находим ускорение груза:

                                                        .                                 (3)

Если силами трения можно пренебречь, то момент силы, приложенной к системе, равен произведению силы натяжения нити  на ее плечо r относительно оси вращения, равное радиусу диска:     .                                                             (4)

Запишем основное уравнение динамики вращательного движения твердого тела вокруг неподвижной оси:  M = J ε (где ε – угловое ускорение диска 5, а – момент инерции диска) для диска:

                                                   ,                                            (5)

Тангенциальное ускорение а_τ диска в точке отрыва нити направлено в ту же сторону, что и ускорение груза . Следовательно, между угловым ускорением вращения системы и линейным ускорением груза имеется связь:

                                                                                (6)

Уравнения (3) и (6) образуют систему из двух уравнений, позволяющую найти неизвестные величины a и .

                                                                                           (7)

Решая ее, получим: 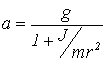                 .                                       (8)

Из формулы (8) следует, что движение груза является равноускоренным. Если в начальный момент груз покоился, то через время t он пройдет путь:

                                                                                                   (9)

Решая уравнения (8) и (9), находим значение момента инерции маятника Обербека  – без грузов на стрежнях и  – с грузами на стрежнях:

                                           .                                    (10)

Момент инерции силы с учетом теоремы Гюйгенса-Штейнера можно рассчитать, применяя формулу:

                                               ,                                   (11)

где  – суммарный момент инерции двухступенчатого диска, втулки и стержней крестовины 4МR² – момент инерции подвижных грузов 2, R – расстояние от центра масс груза на стержне до оси вращения O.

Выполнение работы

1. Определить момент инерции  системы без грузов на стержнях. Для этого измерить время t₀ прохождения этим грузом некоторого фиксируемого пути h и воспользоваться формулой (10). Время t₀ = t определить как среднее на основании пяти измерений.

2. Результаты измерений п. 1 занести в таблицу 1.