Опытная проверка теории плоского поперечного изгиба (лабораторная работа)

КЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ИНЖЕНЕРНОЙ МЕХАНИКИ

УТВЕРЖДЕНО

На заседании кафедры

Протокол № ________

От __________ 2008 г.

ЛАБОРАТОРНАЯ РАБОТА № 8

по курсу: «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ»

ОПЫТНАЯ ПРОВЕРКА ТЕОРИИ ПЛОСКОГО

ПОПЕРЕЧНОГО ИЗГИБА

Керчь  2008г.

1. ЦЕЛЬ РАБОТЫ

Проверка соответствия теории плоского изгиба путем сравнения результатов теории с результатами эксперимента деформаций консольной балки.

2. КРАТКИЕ СВЕДЕНИЯ

В теории плоского поперечного изгиба используются зависимости, полученные при чистом изгибе.

Так, нормальные напряжения в поперечном сечении балки определяются по формуле Навье:

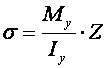;                 (1)

где    М_у – изгибающий момент в сечении Нм

I_y – момент инерции сечения относительно нейтрального, м²

Z – координата слоя, в котором определяют напряжения

Перемещение поперечных сечений балки определяется с помощью дифференциального уравнения изогнутой оси балки:

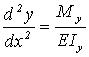                    (2)

где:  у – прогиб балки

         х – текущая координата сечения балки

Приведенные выражения, полученные для чистого изгиба, не отражают истинную картину напряженно-деформированного состояния балки при плоском изгибе, потому что не учитывают влияния поперечной силы. Под действием поперечной силы продольные волокна взаимодействуют друг с другом, а поперечные сечения не остаются плоскими, т.е. гипотеза плоских сечений утрачивает свое значение. Материал балки не находится в линейном напряженном состоянии как при чистом изгибе, а будет иметь место плоское напряженное состояние.

Выполненные исследования показывают, что при плоском изгибе, возможно, пользоваться формулами, полученными для чистого изгиба, ошибки при этом получаются небольшими, и ими можно пренебречь в большинстве случаев.

С точки зрения проверки теории лучше пользоваться выражением (1), позволяющим определить напряжение в точке, однако приборов, позволяющих с высокой точностью измерять этот параметр – нет. Механические тензометры, позволяющие измерять абсолютную деформацию имеют довольно значительную базу = 10…20 мм (тензометр Гуггенбергера, тензометр Апетова), что конечно далеко от точки, если учитывать незначительные размеры лабораторных балок, тоже относится и к омическим электротензометрам. Полупроводниковые тензометры серии Ю имеют базу сравнимую с точкой = 2…3 мм, однако они дефицитны и дороги, к тому же требует специальных схем по термокомпенсации т.к. имеют большую температурную нестабильность.

Учитывая вышесказанное, для проверки теории плоского изгиба будем пользоваться дифференциальным уравнением изогнутой балки (2). Интегрируя это уравнение, определяет угловую и линейную деформации сечения, определяемого координатой Х, значение которой можно определить с высокой точностью. Угловая и линейная деформации сечения также определяются с высокой точностью, применением индикаторов часового типа.

3. ЛАБОРАТОРНАЯ УСТАНОВКА

Установка (рис.1) состоит из основания (7), к которому жестко закреплена стальная балка (1). Балка (1) может нагружаться грузами (2). Положение груза (2) по отношению к заземленному концу может изменяться (размер «а»). Прогиб в конечном сечении, определяемом размером , измеряется с помощью индикатора часового типа (3), установленного на штативе (4). Угол поворота конечного сечения вычисляют по показаниям индикатора часового типа (6) на длине =155мм, передаваемого с помощью планки (5).