Попадание точек в область, ограниченную тремя линиями

1. СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ

1.1 Формулировка условия задачи

"Попадание точек в область, ограниченную тремя линиями"

            Заданы уравнения трех кривых на координатной плоскости (см. таблицу 1). Одно из уравнений содержит переменный коэффициент k. Кривые, пересекаясь, ограничивают замкнутую область D (область 1 на рис. 1), размеры которой зависят от значения коэффициента k. Известны начальное значение k _нач , конечное значение k _кон  и шаг изменения — Dk;

            На той же плоскости заданы координаты n точек, образующих множество М (координаты задаются произвольно, n £ 20).

            Для каждого из заданных значений k сформировать подмножество P Í M, содержащее точки, которые находятся внутри замкнутой области D.

Таблица 1

1.2 Пример решения задачи

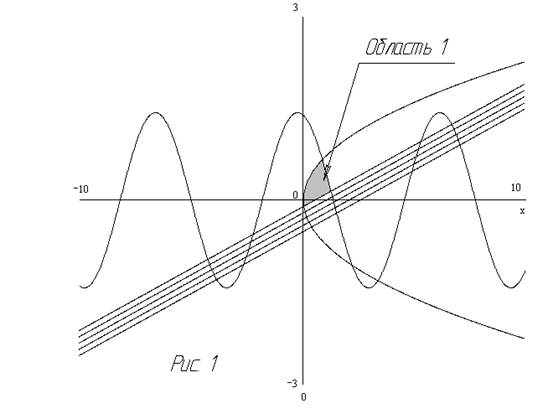Для решения задачи построим заданные кривые на декартовой плоскости и определим получающиеся при их пересечении зоны. На рис. 1 показаны парабола, косинус и семейство прямых, соответствующих значениям коэффициента k. Видно 5 областей, ограниченных всеми тремя кривыми, из них мы будем рассматривать одну (область 1). Эта область содержит точку (0.25,0.25). Теперь решением задачи будут все точки, входящие в закрашенный участок.

2. Формализованная постановка задачи

2.1. Способ получения результатов по исходным данным

            Для установления принадлежности рассматриваемой точки из множества М области 1 на декартовой плоскости, нам необходимо выяснить положение данной точки относительно каждой кривой, лежит ли она ниже или выше. Для этого сравниваем ординату точки и значение функции от значения абсциссы точки. Если больше ордината, то точка лежит «выше» графика функции, соответственно и наоборот. Проверка совокупности таких условий и составляет содержание решения задачи, так как для данной области, ограниченной кривыми, отношения, что выше – данная кривая или данная точка – постоянны. Другими словами (см. рис.1 в п. 1.2), любая точка в помеченной области лежит ниже графика косинуса, и это состояние «меньше»/«ниже» в пределах зоны не может измениться. Теперь очевидно, что совокупность отношений «выше» и «ниже» к разным кривым однозначно задает область на плоскости, значит, для определения принадлежности точки указанному множеству можно установить, выполняется ли набор таковых условий для координат или не выполняется.

            Необходимо заметить, что для корректного следования этому подходу надо все заданные уравнения кривых привести к виду функций y(x). Работая с однозначными функциями легче определить высоту точки над ней. В задании на курсовую работу есть многозначная функция: лежачая парабола y²=0.5x. Разобьем ее на 2 функции:

éy= – Ö(x/2)

ëy=    Ö(x/2)

            К особому случаю следует отнести тот, при котором абсцисса точки не лежит в области определения одной из функций (у нас это пара функций y= ± Ö(x/2), остальные определены на R). Для таких точек выcказывание «выше» или «ниже» не имеет смысла, так как здесь функции не существует. Исходя из эскиза картины на плоскости, можно сказать, что область (1) находится правее x=0, и точки, абсциссы которых лежат вне области определения, (то есть не лежат в (0, +µ)), заведомо не входят в область 1.

2.2 Описание метода решения задачи

Руководствуясь схемой решения из пункта 2.1, для каждой из точек надо провести исследование, выполняется ли набор условий или нет, кроме того, должна проверяться область определения функции. Реализация перебора всех точек осуществляется циклом for от 1 до числа точек, в теле цикла проверяются условия if: на принадлежность области определения и на соответствие критериям вхождения в область 1 — далее выводим итог.