



линейных цепях свободный процесс описывается линейными
дифференциальными уравнениями, и его вид определяется корнями
характеристического уравнения (собственными частотами цепи ![]() ).
).
|
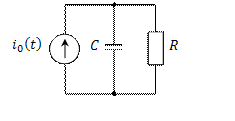 
а) б) |
||
|
Рис. 1 |
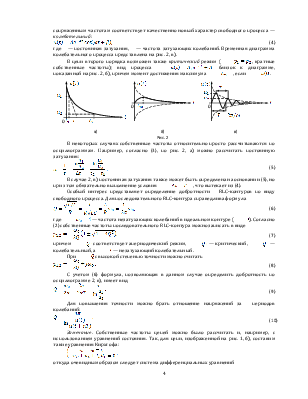
При возбуждении цепи источником тока собственные частоты можно
рассчитать как нули входной проводимости ![]() :
:
1. для цепи первого порядка, изображенной на рис. 1, а),
![]()
откуда получим
|
|
(1) |
2. для цепи второго порядка, изображенной на рис. 2, б),
![]()
откуда
|
|
(2) |
где
![]()
Общий вид решения для напряжения любого элемента цепи
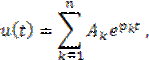
где ![]() — постоянные интегрирования,
— постоянные интегрирования, ![]() — порядок цепи.
— порядок цепи.
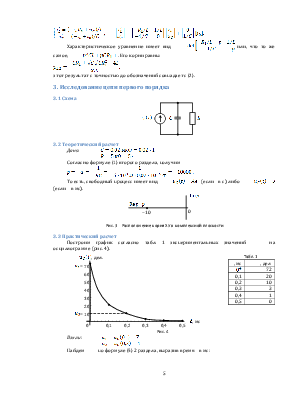
У цепи первого порядка одна собственная частота (1), вещественная и отрицательная, свободный процесс имеет вид
|
|
(3) |
процесс экспоненциальный, причем ![]() — постоянная затухания, а
— постоянная затухания, а ![]() — постоянная времени экспоненты. Временная
диаграмма свободного процесса показана на рис. 2, а), причем
— постоянная времени экспоненты. Временная
диаграмма свободного процесса показана на рис. 2, а), причем ![]() — интервал времени, соответствующий любой
подкасательной к экспоненте.
— интервал времени, соответствующий любой
подкасательной к экспоненте.
В цепи второго порядка две собственные частоты (2) могут быть вещественными (апериодический режим; временная диаграмма суммы двух экспонент, изображенных пунктиром, показана на рис. 2, б) или комплексно-сопряженными. Комплексно-сопряженным частотам соответствует качественно новый характер свободного процесса — колебательный:
|
|
(4) |
где ![]() — постоянная затухания,
— постоянная затухания, ![]() — частота затухающих колебаний. Временная
диаграмма колебательного процесса представлена на рис. 2, в).
— частота затухающих колебаний. Временная
диаграмма колебательного процесса представлена на рис. 2, в).
В цепи второго порядка возможен также критический режим (![]() , кратные собственные частоты); вид
процесса
, кратные собственные частоты); вид
процесса ![]() близок к диаграмме, показанной на рис. 2,
б), причем момент достижения максимума
близок к диаграмме, показанной на рис. 2,
б), причем момент достижения максимума ![]() , если
, если ![]() .
.
|
а) б) в) |
|
Рис. 2 |
В некоторых случаях собственные частоты относительно просто рассчитываются по осциллограммам. Например, согласно (3), по рис. 2, а) можно рассчитать постоянную затухания:
|
|
(5) |
В случае 2, в) постоянная затухания также может быть определена на
основании (5), но при этом обязательно выполнение условия
![]() , что вытекает из (4).
, что вытекает из (4).
Особый интерес представляет определение добротности ![]() RLC-контуров по
виду свободного процесса. Для последовательного RLC-контура
справедлива формула
RLC-контуров по
виду свободного процесса. Для последовательного RLC-контура
справедлива формула
|
|
(6) |
где ![]() — частота незатухающих колебаний в
идеальном контуре (
— частота незатухающих колебаний в
идеальном контуре (![]() ). Согласно (2)
собственные частоты последовательного RLC-контура можно
записать в виде
). Согласно (2)
собственные частоты последовательного RLC-контура можно
записать в виде
|
|
(7) |
причем ![]() соответствует апериодический режим,
соответствует апериодический режим, ![]() — критический,
— критический, ![]() — колебательный, а
— колебательный, а ![]() — незатухающий колебательный.
— незатухающий колебательный.
При ![]() с высокой степенью точности можно считать
с высокой степенью точности можно считать
|
|
(8) |
С учетом (6) формула, позволяющая в данном случае определить добротность по осциллограмме 2, в), имеет вид
|
|
(9) |
Для повышения точности можно брать отношение напряжений за ![]() периодов колебаний:
периодов колебаний:
|
|
(10) |
Замечание. Собственные частоты цепей можно было рассчитать и, например, с использованием уравнений состояния. Так, для цепи, изображенной на рис. 1, б), составим такие уравнения Кирхгофа:
![]()
откуда очевидным образом следует система дифференциальных уравнений
![]()
Характеристическое уравнение имеет вид ![]() или, что то же самое,
или, что то же самое, ![]() . Его корни равны
. Его корни равны
![]()
этот результат с точностью до обозначений совпадает с (2).
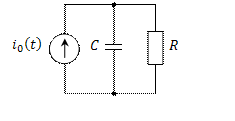
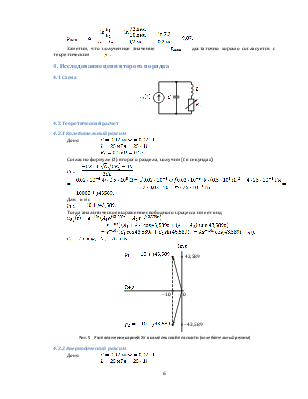
Дано: ![]()
![]()
Согласно формуле (1) второго раздела, получим
![]()
То есть, свободный процесс имеет вид ![]() (если
(если ![]() в с) либо
в с) либо ![]() (если
(если ![]() в мс).
в мс).
|
|
|
Рис. 3 Расположение корня ХУ в комплексной плоскости |
Построим график согласно табл. 1 экспериментальных значений ![]() на осциллограмме (рис. 4).
на осциллограмме (рис. 4).
|
||||||||||||||||
|
Рис. 4 |
||||||||||||||||
Взяли: ![]()
![]()
Найдем ![]() по формуле (5) 2
раздела, выразив время
по формуле (5) 2
раздела, выразив время ![]() в мс:
в мс:
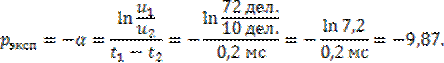
Заметим, что полученное значение ![]() достаточно хорошо согласуется с
теоретическим
достаточно хорошо согласуется с
теоретическим ![]() .
.
Дано: ![]()
![]()
![]()
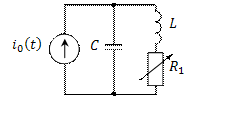
Согласно формуле (2) второго раздела, получим (t в секундах)
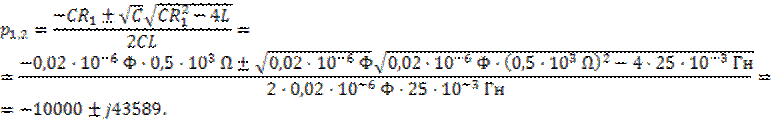
Для ![]() в мс
в мс
![]()
Тогда аналитическое выражение свободного процесса имеет вид
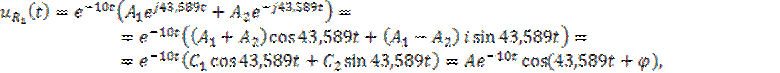
![]()
|
|
|
Рис. 5 Расположение корней ХУ в комплексной плоскости (колебательный режим) |
Дано: ![]()
![]()
![]()
Согласно формуле (2) второго раздела, получим (t в секундах)
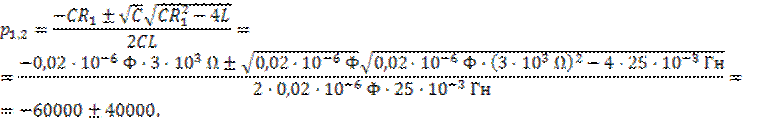
Для ![]() в мс:
в мс: ![]() ,
, ![]() ,
, ![]() .
.
Тогда свободный процесс имеет аналитическое выражение
![]()
|
|
|
Рис. 6 Расположение корней ХУ в комплексной плоскости (апериодический режим) |
|
||||||||||||||||||||||
|
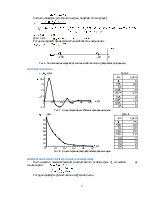
Рис. 7 Осциллограмма колебательного режима цепи |
||||||||||||||||||||||
|
||||||||||||||||||||||
|
Рис. 8 Осциллограмма апериодического режима цепи |
||||||||||||||||||||||
Воспользуемся осциллограммой колебательного режима (рис. 7),
и возьмем ![]() из соображения
из соображения ![]() :
:
![]()
![]()
Тогда, по формуле (5) постоянная затухания равна:

Собственная частота колебаний равна, очевидно,
![]()
Отсюда (для t в секундах) собственные частоты равны:
![]()
Для ![]() в мс, соответственно,
в мс, соответственно, ![]() .
.
Как видно из сравнения результата с теоретическим (п. 4.2.1),
наибольшая ошибка наблюдается при вычислении колебательной составляющей ![]() периодического процесса.
периодического процесса.
Как и в предыдущем пункте, возьмем
![]()
![]()
и воспользуемся формулой (9) раздела 2:
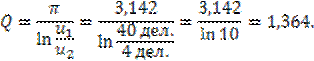
Вывод: происходит колебательный процесс (1,364 > 0,5); вместе с тем 1,364 < 10, значит, колебания в системе затухают весьма быстро. Это можно наблюдать и на осциллограмме (рис. 7).
Выполнив данную лабораторную работу, мы изучили связь между видом свободного процесса в электрической цепи и расположением собственных частот на комплексной плоскости. Нами были приближенно вычислены (по осциллограммам) собственные частоты для цепи первого порядка и цепи второго порядка в колебательном режиме. Мы также оценили добротность RLC-контура (цепь второго порядка) по осциллограмме колебательного процесса.
Как видно из предыдущих пунктов работы, для цепи первого порядка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.