Исследование дифференцирующей и интегрирующей цепей

Министерство образования и науки Российской Федерации

Федеральное государственное автономное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский государственный университет аэрокосмического приборостроения»

ОТЧЕТ
ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Доцент, к.т.н.				Малинин С.И.
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

Лабораторная работа 2 ИССЛЕДОВАНИЕ ДИФФЕРЕНЦИРУЮЩЕЙ И ИНТЕГРИРУЮЩЕЙ ЦЕПЕЙ

по курсу: Радиосистемы передачи информации

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ  ГР.	2946				Кузьмина Елена
			подпись, дата		инициалы, фамилия

Санкт-Петербург
2013

      1. Цель работы

         Экспериментальное исследование преобразований форм прямоугольных импульсов с помощью дифференцирующей и интегрирующей цепей.

      2. Основные теоретические положения

         Дифференцирующей цепью является линейный четырех­полюсник, напряжение на выходе которого пропорционально первой производной входного напряжения:

                        .         

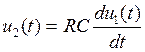        На рис.2.1 приведенасхема дифференцирующей цепи. Напряжение на входе u₁в соответствии со вторым законом Кирхгофа равно

u₁=u_C+u_R .

        Цепь RC будет представлять собой дифференцирующую, если u_R<<u_C , т. е. ес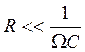ли

                           или .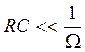                        

                              

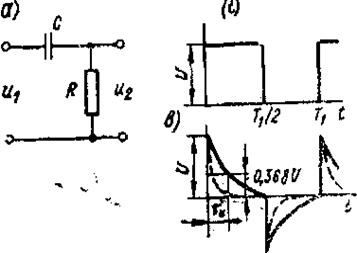
Рис. 2.1

        Если на входе подается напряжение прямоугольной формы, то напряжение на выходе будет изменяться по за­кону

                                    .

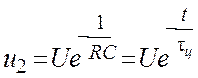        Чем меньше постоянная времени т_ц, тем больше выход­ное напряжение приближается к идеальной форме продиф­ференцированного сигнала. Постоянная времени цепи, оче­видно, соответствует времени, за которое напряжение умень­шается в 1/е раз, т. е. составляет 0,368U (рис. 2.1).

        Интегрирующей цепью называется линейный четырехпо­люсник, напряжение на выходе которого пропорционально интегралу от входного напряжения:

                                     .

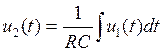          На рис. 2.2 изображена интегрирующая цепь RC.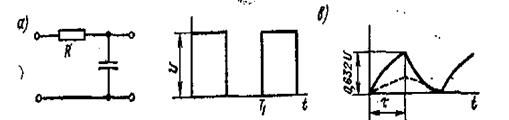         

                                       Рис. 2.2

       При выполнении условия

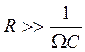                        или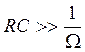                               

можно написать, что ток в цепи

                    

        Предположим, что на вход цепи (рис. 2.2, а) подано напряже­ние, изображенное на рис. 2.2, 6. Тогда напряжение на выходе этой цепи  будет изменяться при ,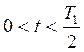   

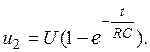
        На рис. 2.2, в сплошной линией изображено напряжение на выходе цепи, в которой τ_ц = RC = T₁/2. В момент t= Ti/2 напряжение на выходе

                            

        При идеальном интегрировании прямоугольного импульса напряжение без учета потерь мощности должно бы нара­стать по линейному закону (пунктирная линия). Чем больше будет постоянная времени цепи τ_ц относительно длительности импульса τ, тем больше интегрирующая цепь будет прибли­жаться к идеальной.

3. Методика выполнения работы

3.1 Изменение напряжения

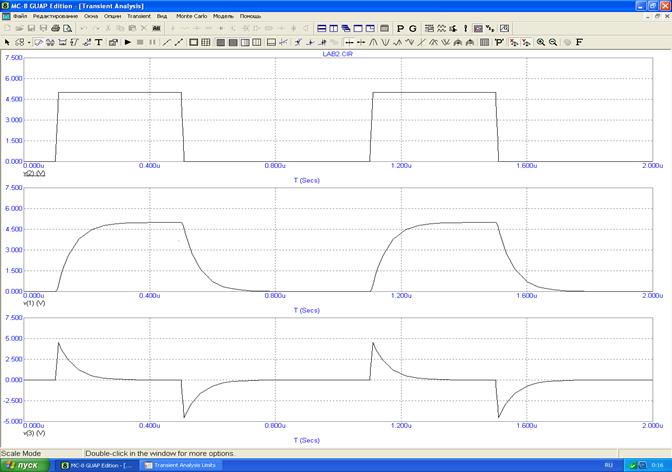
               3.2. Исследование преобразования напряжения на выходе цепи для трех значений R. Определение постоянных времени τ_ц иссле­дуемых цепей.

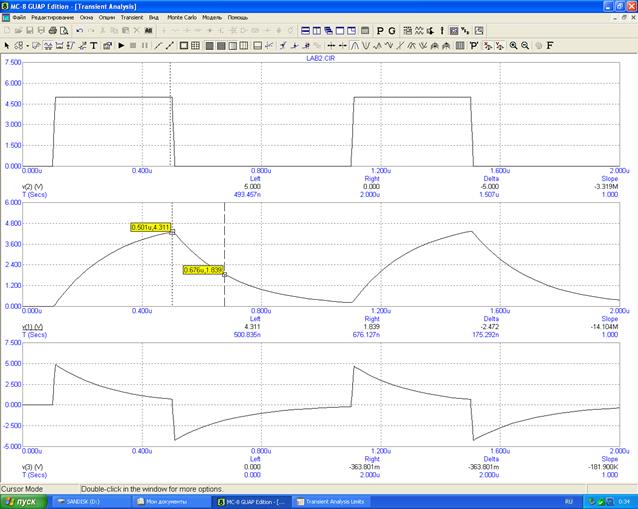
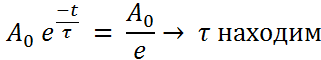
1) 

2) 

3) 

3.3 Определение постоянных времени τ_ц иссле­дуемых цепей при помощи касательной.

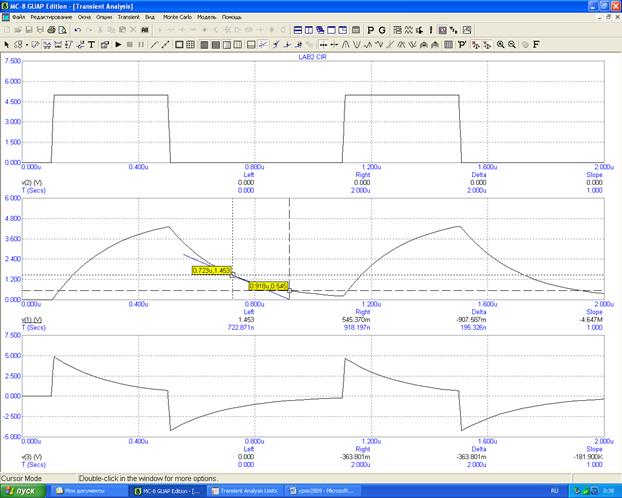
3.4  Подаем  на вход гармоническое колебание и определяем сдвиг фаз Φ между  входным и выходным напряжениями дифференцирующей цепи.

  

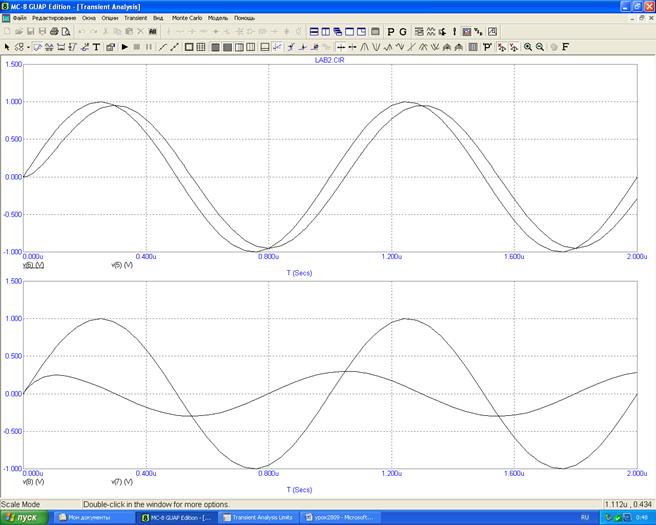
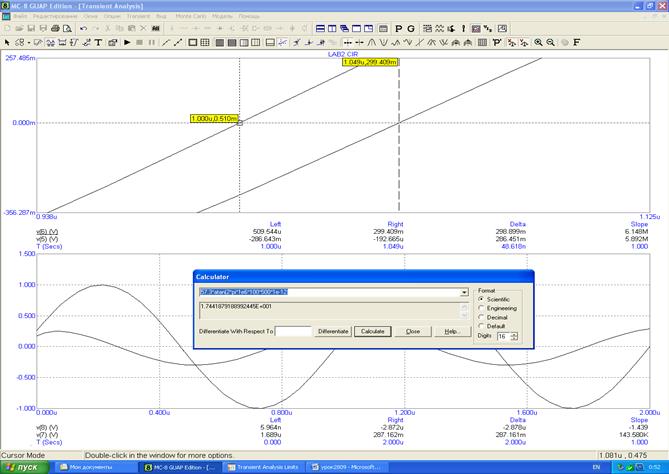
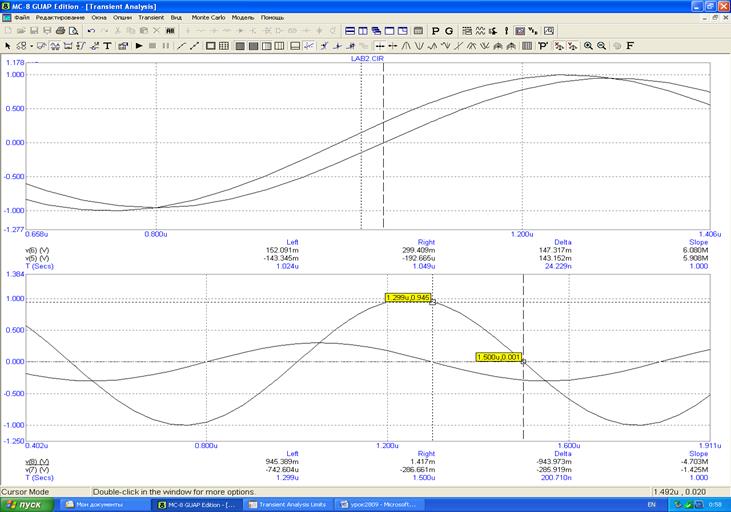
                          U_R

                                                   

                                         β

Uc                 α

1)

2)

3)

Вывод:

В данной работе мы исследовали преобразования форм прямоугольных импульсов с помощью дифференцирующей и интегрирующей цепей.

Определили  постоянные времени τ_ц иссле­дуемых цепей.

Определили  угол сдвига фаз Φ между входным и вы­ходным  напряжениями гармонического колебания дифференцирующей цепи при условии подачи на вход гармони.