Изучение свойств Т-волны в коаксиальной линии, страница 2

Рис. 2.

в окно схемы элемент COAX. Выбрав в меню Draw/ Add Groundэлемент

заземления, мы заземлили оба конца экрана отрезка коаксиала. Вернувшись на вкладку Elements, мы выбрали в категории Lumped Element/ Resistor элемент Load (нагрузка) и мышью поместили его на выход коаксиала. В конце к схеме мы подсоединили порт, находящийся в категории Port (или через меню Draw/ Add Port).

Параметры всех элементов схемы мы установить в соответствии с заданием (см. п. 3.1).

Далее был задан расчёт и отображение комплексного входного импеданса.

В меню Options/ ProjectOptions мы установили указанный диапазон частот (0 – 3  с шагом  0,05 [ГГц]).

В созданном проекте MicrowaveOffice для заданного значения f₀ = 3 [ГГц], заданного варианта отрезка коаксиальной линии (l ≈ 150 [мм]) и набора значений сопротивления нагрузки R = 0, Z₀/2, Z₀, 2Z₀, 1000Z₀ мы провели ряд расчётов.

3.2.1. Расчёт значения модуля входного коэффициента отражения и КСВ.

Расчёт значения модуля входного коэффициента отражения и КСВ проводился следующим образом:

ρ_н = 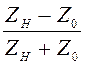; КСВ = 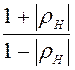 (в нашем случае Z_н = R).

Результаты расчётов по этим формулам сведены в табл. 3.

                                                                   Таблица 3

Пример расчёта (для Z_н = R = 1000Z₀):

ρ_н = 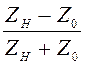= = 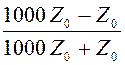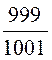≈ 0,998; КСВ = 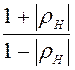= ≈ 999.

3.2.2. Построение семейства графиков зависимостей вещественной и мнимой частей  входного сопротивления отрезка коаксиала с вышеуказанными нагрузками.

Семейства указанных графиков были построены в среде программы MicrowaveOffice в полосе частот 0…10 [ГГц].

Полученные графики представлены на рис. 3 – 7 (рис. 3 – для R = 0, рис. 4 – для  R = Z₀/2, рис. 5 – для R = Z₀, рис. 6 – для R = 2Z₀ и рис. 7 для R = 1000Z₀).

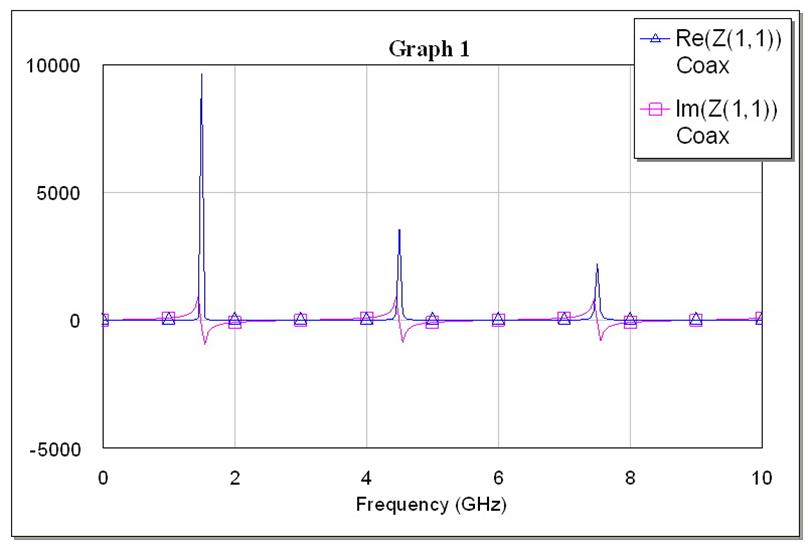
Рис. 3. Зависимость вещественной и мнимой частей  входного сопротивления отрезка коаксиала с нулевым сопротивлением нагрузки от частоты.

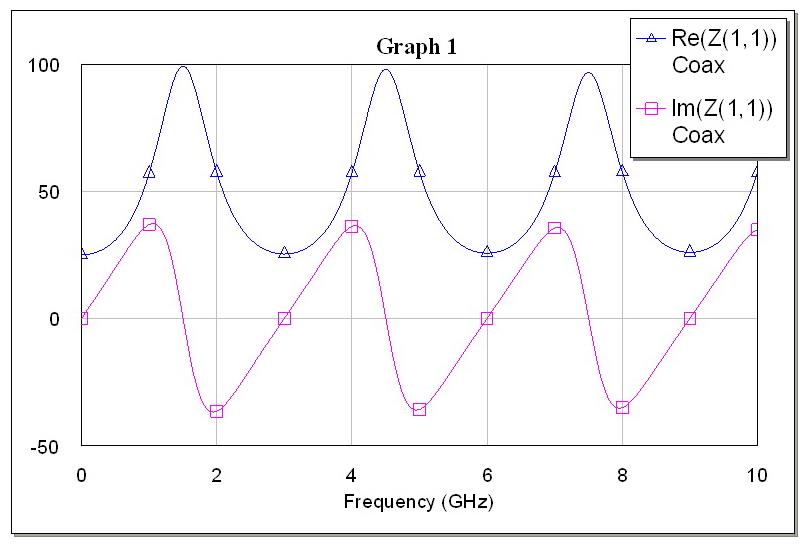
Рис. 4. Зависимость вещественной и мнимой частей  входного сопротивления отрезка коаксиала с сопротивлением нагрузки, равным Z₀/2, от частоты.

Рис. 5. Зависимость вещественной и мнимой частей  входного сопротивления отрезка коаксиала с сопротивлением нагрузки, равным Z₀, от частоты.

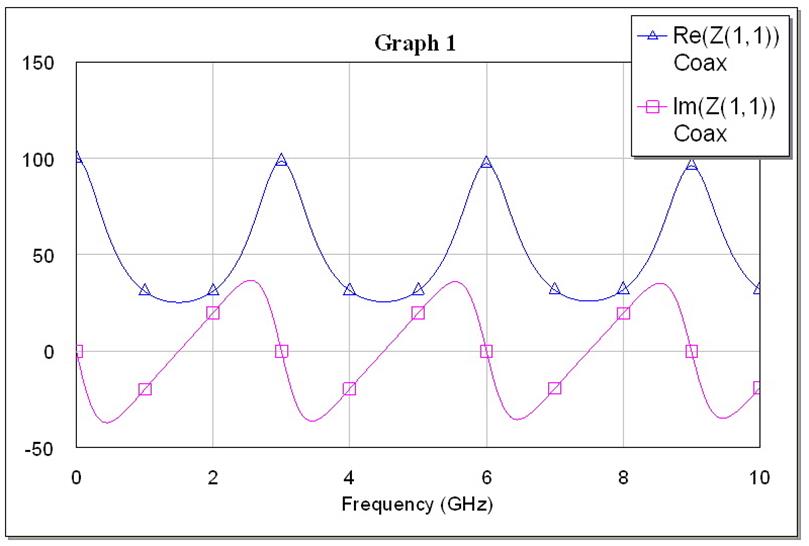
Рис. 6. Зависимость вещественной и мнимой частей  входного сопротивления отрезка коаксиала с сопротивлением нагрузки, равным 2Z₀, от частоты.

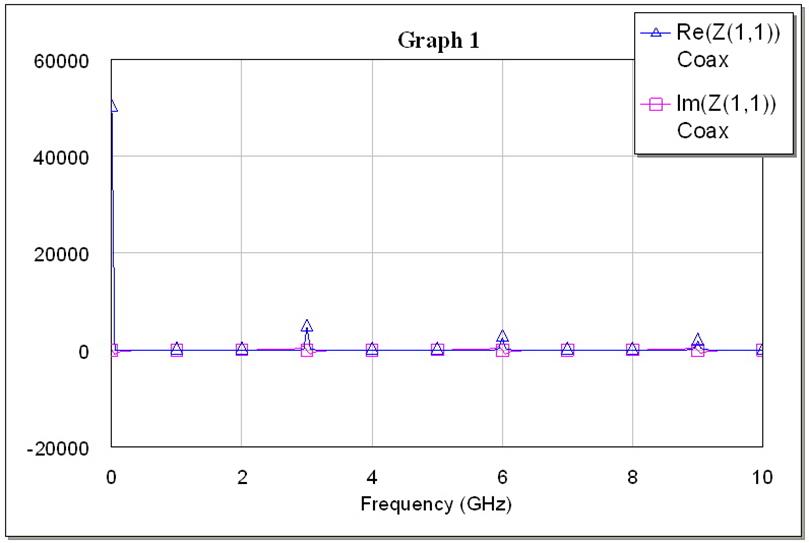
Рис. 7. Зависимость вещественной и мнимой частей  входного сопротивления отрезка коаксиала с сопротивлением нагрузки, равным 1000Z₀, от частоты.

3.2.3. Построение вещественной и мнимой частей входного сопротивления отрезка коаксиала с вышеуказанным сопротивлением нагрузки на круговой диаграмме.

Характеристики из предыдущего пункта были изображены на круговой диаграмме в полосе частот f₀ ± f₀/10 с шагом f₀/20. В результате мы получили пять графиков с круговой диаграммой, см. рис. 8 – 12 (рис. 8 – для R = 0, рис. 9 – для  R = Z₀/2, рис. 10 – для R = Z₀, рис. 11 – для R = 2Z₀ и рис. 12 для R = 1000Z₀).

3.2.4. Изображение на круговой диаграмме изменения входного сопротивления отрезка линии, нагруженного на сопротивление R = Z₀/2, при изменении его электрической длины от 0 до π с шагом π/8.

Для этого мы воспользовались формулой:

z = 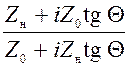, где Θ – электрическая длина отрезка коаксиальной линии.

Результаты представлены в виде табл. 4.

Таблица 4

Данные табл. 4 были отображены на круговой диаграмме, см. рис. 13.

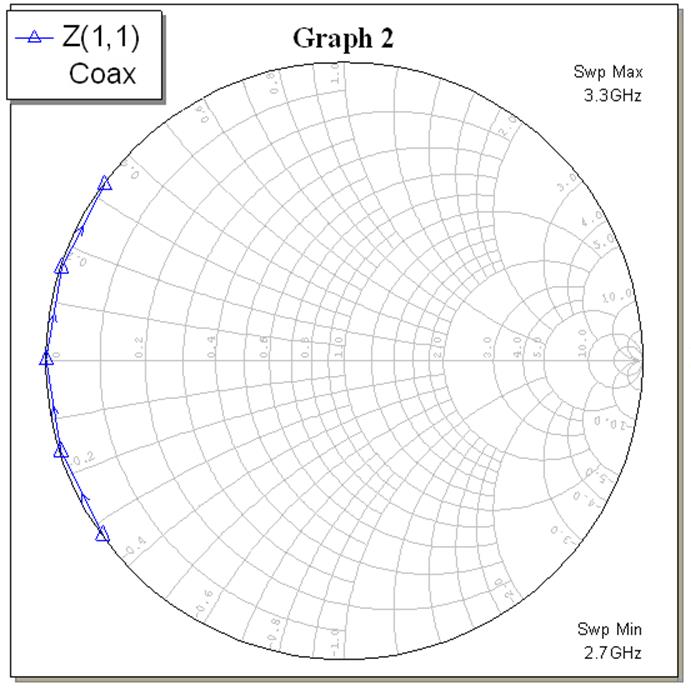
Рис. 8.

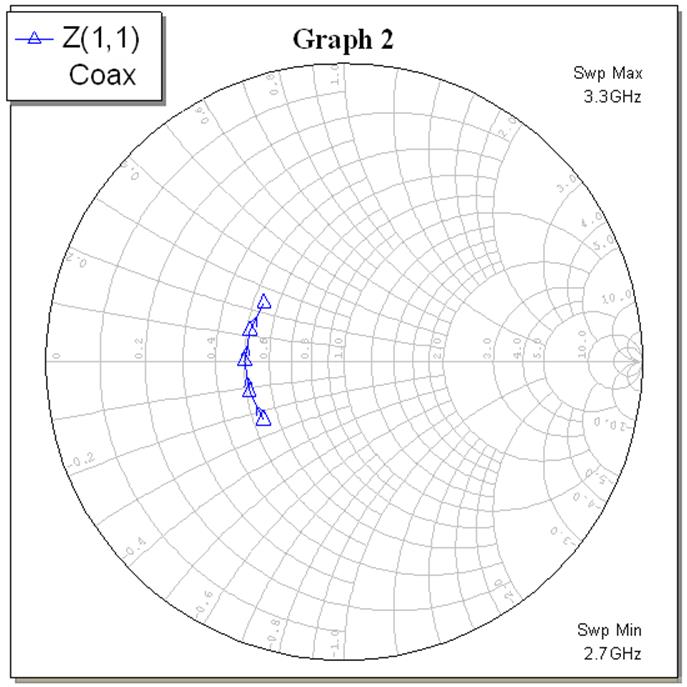
Рис. 9.

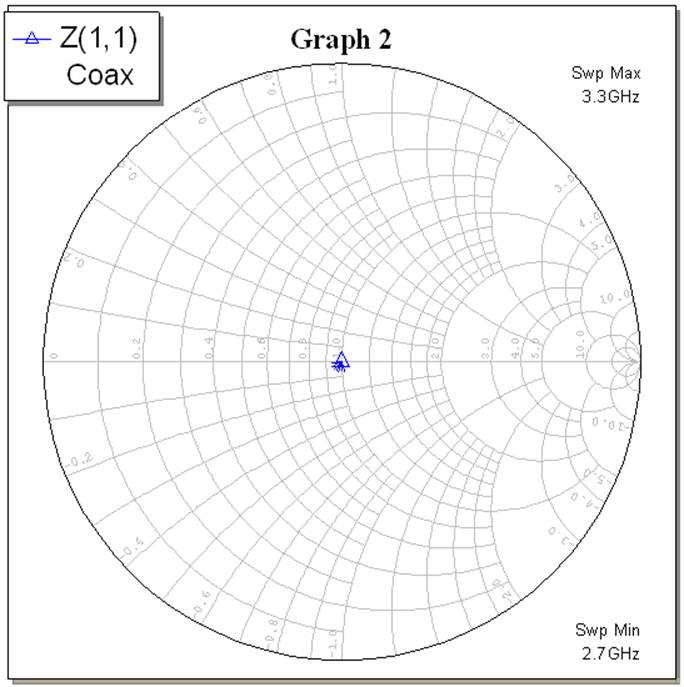
Рис. 10.

Рис. 11.

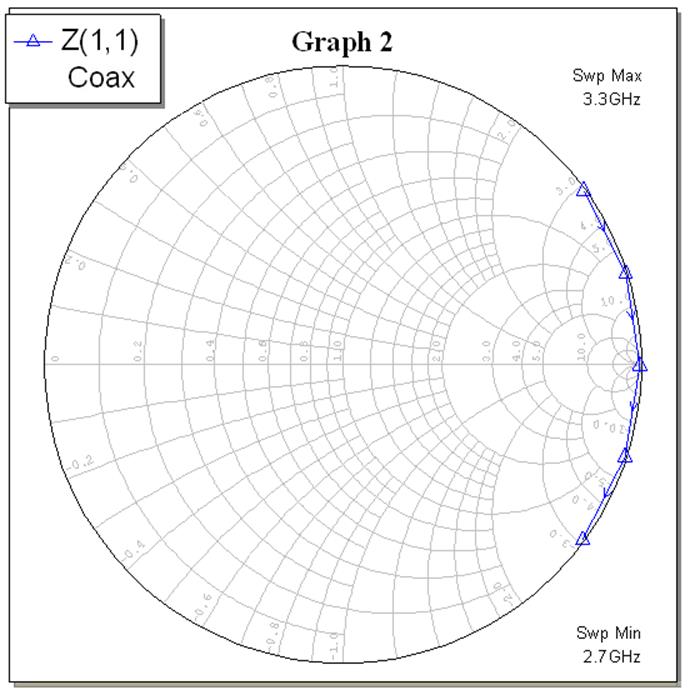
Рис. 12.

4. Выводы.