Новосибирский государственный университет
Экономический факультет
КАК НАИЛУЧШИМ ОБРАЗОМ ПОДГОТОВИТЬСЯ
К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ «ФИНАНСЫ И КРЕДИТ»
М.В. Лычагин, 2011
|
1.1. Задачи на кругооборот оборотных средств
Для успешного решения этих задач надо повторить лекцию 3 и еще раз поработать с тестовой программой (задача 3).
Первым ключевым моментом при решении данных задач является умение находить минимально необходимые запасы для каждого дня при помощи имитационной модели их движения. Не пожалейте времени для того, чтобы довести до автоматизма соответствующий навык решения. При этом постоянно видим перед своим мысленным взором следующую схему:
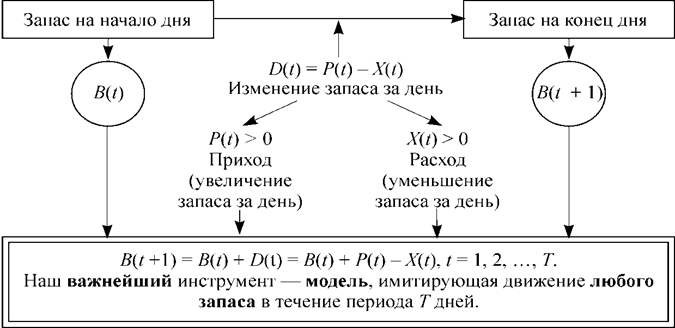
Начнем отрабатывать навык решения по принципу «от простого — к сложному».
Экзотическая иллюстрация. Длительность периода — один календарный день (точнее, одни сутки). Человек (например, Вы) очутились на чудесном тропическом острове, где в изобилии растут бананы. Ничего не поделаешь, приходится питаться одними бананами (хотя они уже надоели и в России). Обозначим через X(t) — число связок (правильнее — соплодий) бананов, которое требуется съесть в день t для того, чтобы нормально себя чувствовать. Предположим, что X(t)= 1 для всех t[1]. Запас связок бананов, находящихся в Вашем распоряжении и готовых к употреблению на начало дня t, обозначим через B(t). Очевидно, что в момент прибытия на остров все бананы растут (B(t) = 0) и их потребуется срезать. Обозначим через P(t) число связок бананов, которые потребуется срезать в день t для пополнения запаса и нормального питания. Вопрос: каким должно быть значение P(t) в каждый день некоторого периода T дней?[2]
Решение. Смотрим на рисунок со схемой запаса. Запас (остаток бананов) на начало дня t + 1 может быть найден по формуле:
|
B(t + 1) = B(t)+ P(t) – X(t). |
Подставляем наши известные значения: B(t + 1) = 0 + P(t) – 1. Если Вы не будете ничего оставлять на следующий день (то есть B(t + 1) = 0), то надо быть готовым каждый день срезать по связке бананов для выполнения последнего равенства: P(t) = 0.
Делаем шаг в усложнении натурально-вещественной конструкции, вводя периодические колебания. Например, если ежедневное срезание утомительно, то можно, опять используя уравнение движения запаса и найти, что надо добывать бананы раз в два дня: P(1) = 2; P(2) = 0; P(3) = 2; P(4) = 0, и т. д. При этом запас на начало каждого нечетного дня будет равен нулю, а четного — единице. Можно проиграть и колебания потребления: сегодня съедаем две связки, а завтра устраиваем разгрузочный день.
Нетрудно видеть, что здесь налицо известная задача управления запасами (сразу в динамической постановке): каков должен быть оптимальный объем пополнения запаса, чтобы минимизировать суммарные затраты на приобретение ресурса и его хранение.
Давайте здесь вспомним вывод формулы Уилсона.
Задача нахождения оптимальной партии поставки. Предприятию в год требуется М единиц материала. Материал поставляется со склада партиями по Х единиц и расходуется равномерно во времени. Затраты на доставку партии материала не зависят от объема партии и составляют С денежных единиц (ДЕ). Затраты на хранение единицы материала в течение года составляют Н (ДЕ). Требуется найти размер партии Х, при котором сумма затрат на доставку и хранение будет минимальной.
Решение.
1. Находим число партий, которые потребуется привезти за год: ЧП = М/Х.
2. Находим затраты на доставку за год:Zтранс = ЧП * С = М/Х * С.
3. Находим затраты на хранение, учитывая, что запаса будет меняться от Х — максимума в день завоза, до 0 перед очередной партией (то есть в среднем на складе у нас будет Х/2):Zхран = Н * Х/2.
4. Находим суммарные затраты: ZS= Zтранс + Zхран = М/Х * С + Н * Х/2.
5. Вычисляем первую производную от ZS по Х, приравниваем ее к нулю, и из полученного выражения находим оптимальный размер партии поставки:
![]()
![]() – МC/Х2 + Н /2 = 0. X2 = 2MC
/ HX
=
– МC/Х2 + Н /2 = 0. X2 = 2MC
/ HX
= 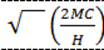
Случай равномерного потребления. Имеется предприятие, которое потребляет один вид материала. Длительность планового периода — 6 дней. Все дни считаются рабочими, а периоды идентичными. На производство продукции по плану ежедневно надо расходовать по одной тонне материала. Перевыполнение плана невозможно, то есть больше одной тонны в день мы произвести не можем. Плановые объемы поставок материала: день 3 — 1 т; день 5 — 2 т; день 6 — 3 т, остальные дни — 0. Время на подготовку материала к запуску в производство — 1 день.
Решение. Оно состоит из 4 этапов:
1. Подготовка таблицы для проведения расчетов (см. табл. 1).
2. Занесение в таблицу исходных и начальных данных (табл. 2).
3. Проведение расчетов при нулевом начальном запасе для определения размера начального запаса при заданных поставках и плановом расходе (табл. 3).
4. Расчет минимального необходимого запаса на начало каждого
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.