Исходя из данных двух таблиц, видно, что факторы “W”, “Q” коррелируют с фактором “L”(>0,75). А зависимость между объясняемой переменной и факторами, показывает, что малозначимый фактор “rub”. Исключая эти два фактора получаем:
Обычный метод наименьших квадратов
(линейная регрессия)
Зависимая переменная: cor3[I]
Количество наблюдений: 50
Переменная Коэффициент Станд. ошибка t-статистика Знач.
1 Константа 0.0270381519 0.0276499981 0.9778717442 [0.3336]
2 cor3[W] 1.0360165298 0.1116375065 9.2801833566 [0.0000]
3 cor3[u] -0.9240740315 0.2623264823 -3.5226105402 [0.0010]
4 cor3[Ur] -0.4196615295 0.1628597114 -2.5768284 [0.0135]
5 cor3[M2] 1.9543898541 0.6692554418 2.9202449947 [0.0056]
6 cor3[Q] 0.6166452506 0.3365688009 1.8321521452 [0.0739]
7 cor3[IPC] 0.3212937053 3.0554595336 0.1051539717 [0.9167]
R^2adj. = 90.244795353% DW = 2.1774
R^2 = 91.439310208% S.E. = 0.0971954541
Сумма квадратов остатков: 0.4062191210011
Максимум логарифмической функции правдоподобия: 49.3752124272333
AIC = -1.6550084971 BIC = -1.3490848162
F(6,43) = 76.54933 [0.0000]
Нормальность: Chi^2(2) = 3.201552 [0.2017]
Гетероскедастичность: Chi^2(1) = 0.556667 [0.4556]
Функциональная форма: Chi^2(1) = 1.569885 [0.2102]
AR(1) в ошибке: Chi^2(1) = 0.439425 [0.5074]
ARCH(1) в ошибке: Chi^2(1) = 0.046983 [0.8284]
Далее видно, что по t-статистике выбывает факторы “IPC”, ”Q”(значение в квадратных скобках больше 0,05 и, следовательно, принимается гипотеза о незначимости фактора). Получаем:
Обычный метод наименьших квадратов
(линейная регрессия)
Зависимая переменная: andru[I]
Количество наблюдений: 50
Переменная Коэффициент Станд. ошибка t-статистика Знач.
1 Константа 0.027306114 0.0153643373 1.7772399398 [0.0823]
2 andru[W] 1.1025437003 0.1064707496 10.355367125 [0.0000]
3 andru[u] -1.0237041183 0.254331223 -4.0250823562 [0.0002]
4 andru[Ur] -0.3917911973 0.1582753264 -2.4753775982 [0.0171]
5 andru[M2] 2.0499602585 0.6421150523 3.192512387 [0.0026]
R^2adj. = 89.933405217% DW = 2.2751
R^2 = 90.755168056% S.E. = 0.098734528
Сумма квадратов остатков: 0.43868281614722
Максимум логарифмической функции правдоподобия: 47.4531145134043
AIC = -1.6581245805 BIC = -1.4286818199
F(4,45) = 110.4396 [0.0000]
Нормальность: Chi^2(2) = 3.227594 [0.1991]
Гетероскедастичность: Chi^2(1) = 0.20341 [0.6520]
Функциональная форма: Chi^2(1) = 3.119931 [0.0773]
AR(1) в ошибке: Chi^2(1) = 1.038509 [0.3082]
ARCH(1) в ошибке: Chi^2(1) = 1.19151 [0.2750]
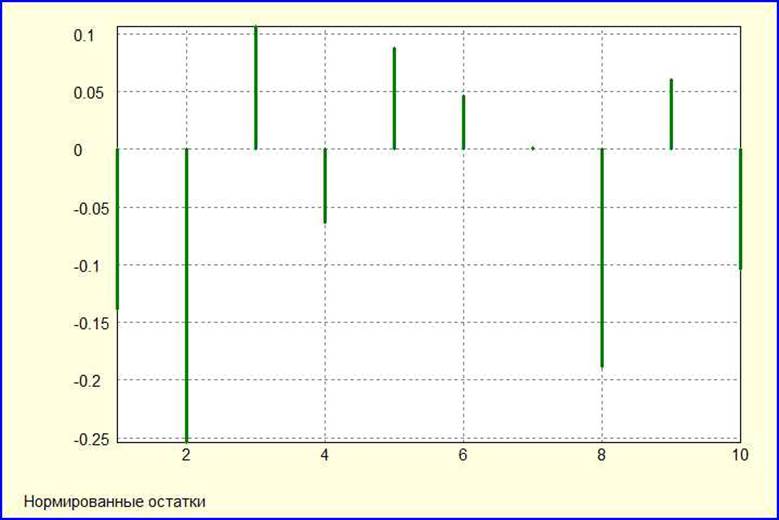
По полученным данным видно, факторы по t-статистике значимы, уравнение регрессии по статистике Фишера значимо (F в квадратных скобках меньше 0,05). Приминается гипотеза об отсутствии автокорреляции первого порядка (AR(1) в ошибке>0,05 в квадратных скобках). Также это можно увидеть, посмотрев DW и рассчитав границы статистики Дарбина-Уотсона (dL= 1,378 и dU=1.721), следовательно, 2.2751 попадает в область (dU;4- dU). Принимается гипотеза о гомоскедастичности (Гетероскедастичность>0,05 в квадратных скобках). Принимается гипотеза о линейности (значение Функциональная форма в квадратных скобках больше 0,05). AIC и BIC нужно минимизировать, чтобы регрессия стала лучше. Критерий χ2 принимает гипотезу о нормальности распределения остатков. Сумма квадратов остатков достаточно мала. По графику автокорреляционной функции остатков можно увидеть, что сильнее всего выражена автокорреляция второго порядка:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.