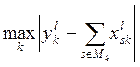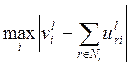
Методы итеративного агрегирования, страница 2

,         

можно судить о степени близости промежуточных решений к глобальному оптимуму.

Если точность приближения не достигнута, то дезагрегацией решения координирующей задачи (15.19) можно получить рекомендуемые верхним уровнем планы и ценностные показатели  в детализированной номенклатуре, которые используются для уточнения параметров локальных задач для следующего этапа расчетов. По решению задач подсистем на каждой итерации уточняются компоненты операторов агрегирования L и Г.

Таким образом, операторы агрегирования L и Г не только преобразуют информационные потоки (сжимая или развертывая состав входной информации), но и определяют направления итеративных расчетов. Приближение промежуточных решений к глобальному оптимуму (решению исходной задачи (15.18))эквивалентно приближению промежуточных операторов агрегирования ,  к операторам "оптимальной структуры" L⁰, Г⁰. Дезагрегацией решения соответствующей сводной задачи (15.19) можно получить детализированное решение исходной задачи (15.18).

Для дальнейших рассуждений удобнее рассматривать операторы преобразования информации L и Г в виде векторов  и  где l_kи  параметры сжатия k-й группы технологических способов и i-й группы условий задачи (15.18) в агрегированные k-йспособ и i-е ограничение.

Пусть ,  - нормированные веса агрегирования:

, ,k=1, …, т; i= 1, ..., п.

Тогда агрегированные показатели строятся следующим образом:

, , , k = 1,…, m; i = 1,…,n            (15.23)

Агрегированная задача имеет вид:

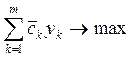
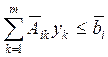
Пусть D — множество весов агрегирования, при которых задача (15.24) разрешима, ,  - решение агрегированной задачи и двойственной к ней,  - значение целевой функции задачи (15.23), (15.24) в оптимальном решении . Справедливо следующее утверждение.

Пусть ,  — решение исходной прямой задачи (15.18) и двойственной к ней,  - отвечающие им веса агрегирования

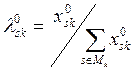, k = 1,…,m

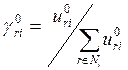, r= 1,…,n

Тогда векторы l⁰, g⁰задают седловую точку функции на множестве D, т.е. для всех ()Î D.

          (15.25)

Свойство оптимальных весов агрегирования позволяет охарактеризовать направление итеративных расчетов. Переход от (l — 1)-й итерации к итерации l должен сопровождаться уменьшением функционала по переменным у и увеличением его по переменным l. Оптимальные планы двойственных агрегированных задач на итерации (l — 1), т.е.  и , выбираются таким образом, чтобы способы двойственных задач, оцененные в этих показателях, были в лучшем случае "безубыточны":

;

.

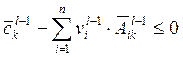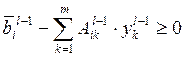Опираясь на свойства симплекс-метода решения задач линейного программирования,можно утверждать, что на итерации l функционал увеличится, если веса агрегирования будут выбраны так, что "новый" k-й агрегированный способ (), рассчитанный по формулам (15.23), будет эффективным в оценках (l- 1)-й итерации:

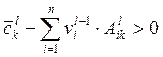          (15.26)

Аналогично, для того чтобы уменьшить функционал F(l,g) по переменным g, необходимо на шаге l выбрать такие веса (),чтобы по некоторым агрегированным ограничениям план шага (l — 1) был невыполним ("сверхрентабельность" в двойственной задаче, рассматриваемой в качестве прямой):

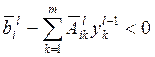
Большинство известных декомпозиционных методов воспроизводят в той или иной форме выражение (15.26) в качестве критерия подсистемы, оптимизирующей свое состояние в детализированных показателях. При использовании методов итеративного агрегирования такой критерий может быть представлен в виде:

.

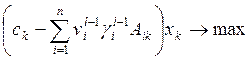Здесь  — вектор дезагрегированных оценок i-й группы условий, получаемых из оценки i-го агрегированного ограничения на шаге (l— 1). Аналогично, вектор  можно рассматривать как рекомендуемый верхним уровнем детализированный план функционирования k-й локальной подсистемы. На основе этих рекомендаций могут быть уточнены задания подсистемам по выпуску продукции в детализированной номенклатуре, скорректированы объемы выделяемых общесистемных ресурсов и т.д. В этом смысле методы итеративного агрегирования включают в себя черты лимитных и ценностных схем согласования плановых решений.

Задачи подсистем выступают в методах итеративного агрегирования не столько "поставщиками" детализированных планов (последние можно получить дезагрегацией сводных планов координирующей задачи), сколько генераторами операторов агрегирования и дезагрегирования информационных потоков.

В качестве примера рассмотрим процесс решения задачи (15.20) методом итеративного агрегирования. Простейшая схема состоит в следующем:

а)            для очередного значения весов агрегирования  по решениям задачи (15.21) и двойственной к ней -  и - рассчитываются детализированные двойственные планы , k= 1, 2; , i = 1, 2.

б)            планы x^l, u^lпроверяются на эффективность используемых способов и сбалансированность по ресурсам:

 < / > 0, k = 1,2;

 < / > 0, i = 1,2;

в) рассчитываются векторы - направления изменения ; в агрегированных способах решения прямой и двойственной задач вес эффективных детализированных способов должен быть увеличен, неэффективных - уменьшен. Это можно учесть следующим образом:

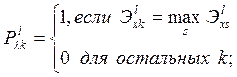
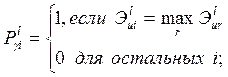
г) новые значения параметров агрегирования ,  рассчитываются обычным образом:

;

.

Здесь ,  — параметры процесса;

д) переход (а).