Межотраслевой натурально-стоимостный баланс (модель, учитывающая организационную структуру народного хозяйства), страница 2

где — объем производства j-й продукции в k-й отрасли; — удельный вес отрасли (ведомства) kв общем объеме производства j-й продукции; при этом ,

Каждой отрасли (ведомству) kсоответствует вектор коэффициентов , jÎJ характеризующих ее специализацию, соотношение профильных и непрофильных видов продукции и т.п.

Третья группа условий — уравнения валовой (товарной) продукции отраслей (ведомств):

, kÎQ                            (7.3)

где — доля товарного выпуска j-й продукции (т.е. учитываемой и валовой и товарной продукции) от общего объема производства этой продукции в k-oй отрасли; — средняя оптовая цена единицы j-й продукции, вырабатываемой на предприятиях k-й отрасли;  — удельный вес прочей продукции отрасли, не выделенной в качестве самостоятельных позиций натурально-стоимостного баланса, в общем объеме валовой (товарной) продукции k-й отрасли.

Совокупность условий натурально-стоимостного баланса (7.1) — (7.3) содержит п + ns+sуравнений и столько же переменных x_j,  х_k (при заданных у_i). В результате расчетов по модели определяются сбалансированные и увязанные с общеэкономическими показателями объемы производства в натуральном выражении (по важнейшим видам продукции) и в стоимостном выражении (по отраслям и ведомствам), потребности народного хозяйства в важнейших видах материальных ресурсов по направлениям их использования.

В дополнение к (7.1) — (7.3) модель может включать ограничения по внешним ресурсам (трудовым ресурсам, основным производственным фондам, производственным мощностям), а также дополняться уравнениями элементов условно-чистой продукции.

Число уравнений и переменных в модели можно сократить путем подстановок. Подставив (7.2) в (7.3), получаем:

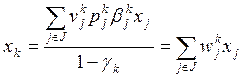            (7.4)

где 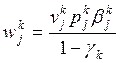 —  общий коэффициент, характеризующий выход валовой (товарной) продукции k-й отрасли с единицы j-и продукции.

"Сжатая" модель включает условия (7.1), (7.4), а расчеты по формуле (7.2) проводятся после определения значений x_j.

Условия (7.4) можно также исключить из основной системы уравнений, подставив их в (7.1) и сделав соответствующие преобразования:

где  означает косвенные затраты i-й продукции на производство единицы j-й продукции, обусловленные производством "нерасшифрованной" продукции.

Вместо (7.1) получаем

, iÎJ (7.5)

или

, iÎJ (7.6)

а в векторно-матричной форме

X = AX + Y                                                                          (7.7)

Y = (E - A)X                                                                         (7.8)

где А = (a_ij+a_ij+σ_ij)- квадратная матрица n-го порядка.

В результате всех преобразований приходим к системе уравнений межотраслевого баланса производства в натуральном выражении. Однако это не возврат к исходной модели межотраслевого баланса (6.11) - (6.14). Существенное преимущество полученной системы уравнений (в любой форме из (7.4) — (7.7) заключается в том, что она сопровождается информацией об организационно-хозяйственной структуре производства (коэффициенты a_ik , a_ii, и полученные на их основе ) - Это позволяет после определения объемов производства в натуральном выражении рассчитывать по формулам (7.2) — (7.4) объемы производства в разрезе хозяйственных отраслей и балансировать объемы производства в натуральном и стоимостном выражении.

Модель натурально-стоимостного межотраслевого баланса непосредственно применяется при разработке годовых и пятилетних народнохозяйственных планов начиная с девятой пятилетки. В 80-х годах плановые натурально-стоимостные балансы охватывали 30 отраслей народного хозяйства и промышленности, 27 промышленных министерств, около 200 продуктов в натуральном выражении.

На начальных этапах плановой работы результаты расчетов по натурально-стоимостному балансу используются в качестве исходных данных для формирования показателей отраслевых и функциональных разделов плана и составления материальных балансов. На заключительном этапе разработки плана натурально-стоимостный баланс используется для проверки взаимной сбалансированности основных показателей развития народного хозяйства. В условиях происходящей перестройки народнохозяйственного планирования натурально-стоимостному балансу отводится важная роль в обосновании системы государственных заказов и их увязке с общеэкономическими пропорциями.