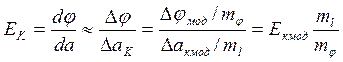 (2.1.1)
(2.1.1)
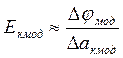 , (2.1.2)
, (2.1.2)
где ∆φмод - разновидность потенциалов между двумя соседними линиями равного потенциала на модели; ∆акмод - расстояние между ними в месте, где рассчитывается напряженность. Вектор напряженности направлен перпендикулярно к линии равного потенциала от большего потенциала к меньшему.
При необходимости картина линий равного потенциала дополняется картиной силовых линий поля. При построении силовых линий необходимо соблюдать следующие правила:
- силовые линии должны быть перпендикулярны поверхности электродов;
- силовые линии должны пересекаться линии равного потенциала под прямым углом;
- криволинейные прямоугольные ячейки картины поля должны быть подобны друг другу, т.е. отношения средних линий ячеек поля должны быть одинаковыми
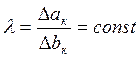 , (2.1.3)
, (2.1.3)
где ∆ак - расстояние между соседними
линиями равного потенциала; ∆bк - расстояние между соседними силовыми линиями поля,
образующими ячейку поля. Две соседние силовые линии образуют силовую трубку
поля, в которой величина потока вектора напряженности поля ∆![]() E постоянна по всей
ее длине. При выполнении условия (2.1.3) все силовые трубки поля будут с одинаковой
∆
E постоянна по всей
ее длине. При выполнении условия (2.1.3) все силовые трубки поля будут с одинаковой
∆![]() Е. Например:
Е. Например:
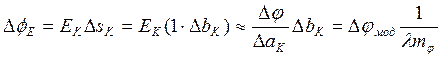 (2.1.4)
(2.1.4)
По их густоте построенных силовых линий можно судить о величине напряженности поля. По картине поля можно определить распределение заряда на поверхности проводящего тела в электрическом поле на границе диэлектрик-проводник Et=O, Dn=eaEn=εaE=σ, получаем с учетом (2.1.1)
 , (2.1.5)
, (2.1.5)
где Екмод определяется по выражению (2.1.2)
в точках вблизи поверхности электрода. Заряд положительный, если вектор ![]() направлен от поверхности, и отрицательный,
если
направлен от поверхности, и отрицательный,
если ![]() направлен к поверхности.
направлен к поверхности.
На этапе сравнения полученных экспериментальных данных с расчетными, мы проводим дополнительный теоретический расчет поля с помощью современных методик расчета (методом конечных элементов, методом конечных разностей, графическим или др.). Расчет может быть выполнен, как альтернатива, с использованием современных компьютерных программ основанных на логике вышеперечисленных методов математического расчета. Наиболее предпочтительны уже упомянутые в пункте 1.5 главы 1 программные комплексы Femlab и ELCUT основанные на МКЭ или МКР. Формирование выводов о результатах моделирования можно путем анализа графиков сходимости результатов теоретических и экспериментальных.
Стоит отметить ещё раз, что предложенная методика исследования ЭМП электродной системы ЭТК не учитывает различные вкрапления в межэлектродной области. То есть принимает в качестве среды находящейся в МЭП ЭТК идеализированную структуру. Вводить в методику исследований учет неоднородной составляющей можно только получения удовлетворительной сходимости расчетных и экспериментальных данных полученных на идеализированной модели. Следовательно, данный аспект можно будет учесть только после многочисленных опытов исследования на предлагаемой экспериментальной модели. Учет этих вкраплений, может быть, достигнут путем введения дополнительных коэффициентов в расчетные формулы, но пока это только догадки.
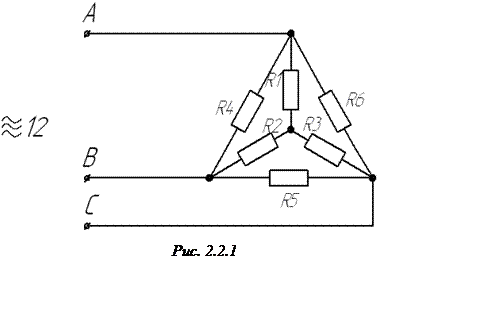 Для определения расхода электроэнергии необходимо проанализировать
характер нагрузки. Можно предположить, что нагрузка является активной. Из курса
электротехники известно, что в трехфазных линиях нагрузка может быть подключена
треугольником, либо звездой. Какой же вид нагрузки представляет предлагаемая
экспериментальная установка. При расположении моделей электродов в виде вершин
треугольника нагрузка представляет собой смешенный вид соединения, то есть
звезда и треугольник одновременно. Если же располагать модели электродов по
прямой, то данный вид нагрузки можно отнести к соединению треугольником.
Проведем расчет нагрузки по методу размещения моделей электродов в
электролитической ванне в вершинах равностороннего треугольника, схема
соединения нагрузки представлена на рис. 2.2.1. Пользуясь данной схемой можно
рассчитать мощность, потребляемую из сети.
Для определения расхода электроэнергии необходимо проанализировать
характер нагрузки. Можно предположить, что нагрузка является активной. Из курса
электротехники известно, что в трехфазных линиях нагрузка может быть подключена
треугольником, либо звездой. Какой же вид нагрузки представляет предлагаемая
экспериментальная установка. При расположении моделей электродов в виде вершин
треугольника нагрузка представляет собой смешенный вид соединения, то есть
звезда и треугольник одновременно. Если же располагать модели электродов по
прямой, то данный вид нагрузки можно отнести к соединению треугольником.
Проведем расчет нагрузки по методу размещения моделей электродов в
электролитической ванне в вершинах равностороннего треугольника, схема
соединения нагрузки представлена на рис. 2.2.1. Пользуясь данной схемой можно
рассчитать мощность, потребляемую из сети.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.