Расчет одноступенчатой колонны промышленного здания. Расчет подкрановой балки

3.5. Расчет одноступенчатой колонны промышленного здания.

      Подбор сечения верхней части колонны . Расчетная комбинация усилий

М=-1315,16 кНм . N=328,4 кН

      Принимаем сечение верхней части колонны в виде сварного двутавра

Высотой h=750мм =75 см.

      Необходимую площадь сечения определяют ориентировочно по формуле

      А_тр=N/R_y(2,25+2,8L/h),

    где L=М/N – эксцентриситет продольной силы относительно оси x-x

      А_тр=328,4/22(1,25+2,8·400/75)=241,57 см²

      Поскольку сечение еще не определено и неизвестны значения его геометрических характеристик (А₁w_x и I_x) для симметричного двутавра принимают

ρ_x=ix²/z=31,5²/0,5·75=26,46 см

ix=0,42·75=31,5 см

      Тогда  m=400/26,46=15,11    

      λ=1148,4/31,5√22/2,1·10,4=1,179

При  значении m>1 и λ<0 для двутаврового сечения.

      heƒ/t_ω<46.34

      beƒ/t_ƒ=14,76

Принимаем высоту стенки h_ω=70 cм, толщину стенки t_ω=1,8 см, ширину полки b_ƒ=40 см и толщину  t_ƒ=1,8 см.

Площадь стенки А_ω=h_ω·ƒ_ω=70·1,8=98 см²

                              Аj=40·1,8=72 см²

      Площадь всего сечения А=72·2+98=153,8 см²

      Находим геометрические характеристики принятого сечения

     I_x=t_ωh_ω³/12=2Aƒ(h_ω/2+t_ƒ/2)²=1,8·70³/12+2·72(70/2+1,8/2)²=22560,53 см⁴

      I_у=2bƒbƒ³/12=21,8·40³/12=19200 см⁴

      W_x=22560,53/35+1,8=6130,57 см³

      I_x=√I_x/A=√22560,53/153,8=12,11 см

      I_y=√I_y/A=√19200/153,8=11,17 см

      λ¯=94,83√22/21000=3,069

      η=1,4-0,02λ¯=1,4-0,02·3,069=1,328

      m_et=1,328·10,11=13,42

      Проверка устойчивости верхней части колонны в плоскости действия момента

                          G_x=N/φ_eA·328,4/153,8·0,097=22 кН/см²<R_yγ_c/γ_n=23,16 кН/см²

Подбор сечения нижней части колонны.

Усилия в ветвях колонны:

      В наружной части N_нв=53,55/1,1·0,4+2333,8/1,1=2143,53кН

      В подкрановой ветви N_пв=328,4/1,1·0,65+3252,7/1,1=3151,05 кН

Определяем ориентировочно требуемую площадь ветвей

      А_тр.п.в.=3151,05/0,8·22=179 см²

         А_тр.п.в.=2143,53/0,8·22=121,79 см²

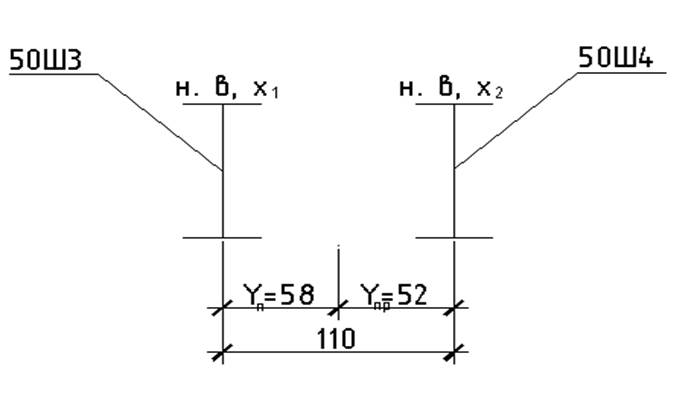
Принимаем наружную ветвь из широкополочного двутавра 50Ш3, а подкрановую из двутавра – 50Ш4

      50Ш3                                       50Ш4   

А=199,20 см²                                   А=221,5 см²

I_y1=84200см⁴                                              I_y2=96150 см⁴

W_y1=3402 см³                                          W_y2=3838 см²                                              

i_y1=20.56 см                              i_y2=20,82 см  

I_x1=9250 см⁴                                               I_x2=10600 см⁴  

W_x1=617 м                                 W_x2=707 см²  

i_x1=6,81 см³                                                  i_x2=6,92

      Находим положение центра тяжести

У_л=223,30·1,1/199,20+221,5=225,30·1,1/420,7=0,58

У_п=1,1-0,58=0,52 м

Расчетные усилия в стержнях

N_нв=53,55/1,1·0,52+2333,8/1,1=25,311+2121,63=2146,94 кН

N_пв=328,4/1,1·0,58+3252,7/1,1=209,5+2957=3166,52 кН

Проверяем устойчивость ветвей как центрально-сжатых стержней.

Наружная ветвь:

В плоскости колонны l_х1=240см.

λ_х1= l_х1/i _х1=240/6,81=35,24

из плоскости колонны i_у1=1398см. λ _у1= l _у1/i _y1=1398/20,56=67,99

По большей гибкости λ _у1=67,99   φ=0,776

G=N_н.в/φА_н.в.=2146,94/0,776·199,2=14,07 км/см²<R_yγ_c/γ_n=22·1/0,95=23,2 кн/см²

 

Подкрановая ветвь:

l_х²=240 см              λ_х2=240/6,92=34,68

из плоскости колонны l_у2=1398  λ_у2=1398/20,82=67,14

Ә=N_пвφА_п.в=3166,52/0,776·221,5=18,4 кн/см²<23,22 кн/см² 

 

Проверка устойчивости колонны как единого стержня составного сечения. Для  этого необходимо найти приведенную гибкость стержня, зависящую от сечения раскосов.

      Раскосы решетки рассчитывают на фактическую поперечную

силу

_Qmax=145,24 к/н               α=42,46^о             sìnα=0,675

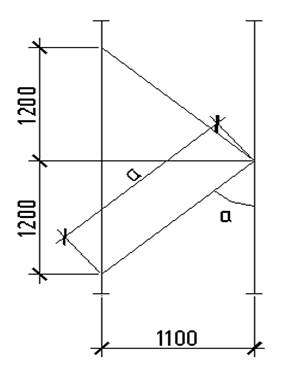
Продольное усилие в раскосе одной плоскости

N_α=Q_max /_2sinα = 145.24/2·0,675=107,6 к/н

Длина раскоса а=√120²+110²=163 см

Требуемая площадь сечения раскоса

А_тр=Nά/φγсR_у=107,6/0,75·0,7·23=8,909 см², где

φ- ориентировочно =0,7

γ_с – коэффициент условия работы = 0,75

Принимаем раскос _└ 106х7 А₁=13,75см²                                                           

i_{min =}1,98cм  λ=163/1,97=81,01  φ=0,682

Напряжение в раскосе

G=107,6/0,682·13,75=1,16<R_yγ_c/γ_n=23·0.75/0.95=18,16кН/cм²

Определяем геометрические характеристики всего сечения колонны и условную предельную гибкость стержня

А=А_.пв+А_н.в.=199,20=221,5=120,7 см²

I_x=(I_x1+А_нву_л²_.)+.(I_хч+А_nв+у_пр²)=(9250+199,2·58²)+(10600+221,5·52²)+679358,8+609536=1288894,8 см⁴   

                i_х=√12888948/420,7=55,35

Гибкость стержня относительно свободной оси х-х

λ_х=1985/55,35=35,86

Приведенная гибкость λ_еƒ=√λ_х²+ά₁·А/А_ά1          =√35,86²+29,82·42,07/27,5=41,7

Α=10·а³/в²ℓ=10·163³/110²·120=29,82

Условная приведенная гибкость

λ_еƒ=λ_еƒ√R_у/Е=41,7√23/21000=1,38

Проверку устойчивости колонны в целом выполним на две комбинации усилий:

Догружающую подкрановую ветвь М₂=3252,7 кНм N=328,4 кН

Догружающую наружную ветвь М₁=+2333,8 кНм;  N=-53,55 кН

Для комбинации усилий, догружающих подкрановую ветвь, относительный эксцентриситет

m_х2=ℓ₂·А/J_х·у_n=3252.70/328.4·420,7·52/1288894,/8=0,168

При m_х2=0,168 и λ_еƒ=1,38 φ_е2=0,83

σ=N₂/φ_е2·А=328,4/420,7·0,83=0,94 кН/см²<R_уγ_с/γ_n=24,2 кН/см²

Для комбинаций усилий, догружающих наружную ветвь, относительный эксцентриситет

M_x1=ℓ₁·A/J_x·y_n=2333,8/53,55·420,7·58/1288894,8=0,82;  φ_е2=0,498

σ =53,55/0,498·420,7=0,255кН/см²<24,2 кН/см²

 

 

Расчет базы колонны.

R_вìℓос=γ·R_в, где

γ- коэффициент зависящий от отношения площади верхнего обреза фундамента к площади опорной плиты, принимаемый не более 1,5

Принимаем бетон класса В15 с R_в=0,85 кН/см² γ=1,2

R_вℓос=1,2·0,85=1,02 кН/см²

Площадь опорной плиты

А_рℓ=3166,52/1,02=3104,43 см²

Принимаем плиту размером 700х500мм, фактическое напряжение под опорной плитой

σ _ℓ.ℓос=N_nв/А_рℓ=3166,52/(70х50)=0,9 кН/см²<R_в.ℓос=1,02 кН/см²

Изгибающий момент на участке плиты 1,

М₁= σ _в.lос·с²/2=0,9·8,8²/2=34,8 кН/см

Изгибающий момент на участке плиты 2, опертом по трем сторонам, будет посередине свободной стороны

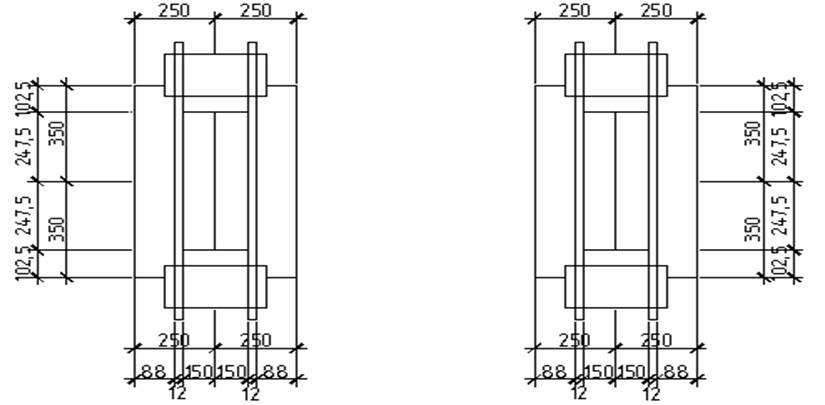
М₂=0,9·10,25²=47,27 кН/см                 σ/в=102,5/300=0,34<0,5

Участок 3. Плита опертая на четыре стороны.

в/а=247,5/150=1,65<2   β=0,088

М₃=0,088·0,9·15²=17,82 кН/см

Требуемая толщина плиты

t_pl=√6М_max/R_у=√6·47,27/21=3,67 см

Где М_max – максимальный момент на рассмотренных участках: R_y=21 кН/см² при t=21…40мм ГОСТ 380-71

Принимаем плиту толщиной 40мм 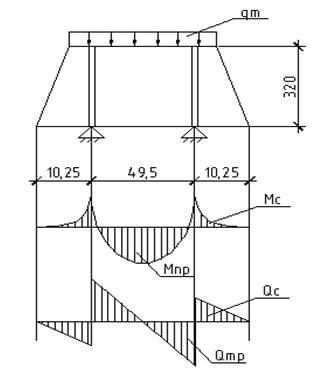                                                                                      Назначаем сечение траверс                                                                                        320х12 и проверяем ее прочность                                                                                        как однопролетной двухконсоль-                                                                                        ной  балки, опирающейся на                                                                                               полки колонны.                                                                                        Равномерно распределенная                                                                                        Нагрузка на траверс.                                                                                      

q_т= σ _в.lос·α_т=09·17,5=15,75 кН/см                                                                                      α_т=150/2+(250-150)=175кН                                                                                        М_с =15,75·10,25²/2=827,36 кН/см                                                                                        М_пр=15,75·49,5²/8=4823,9 кН/см                                                                                        Q_c=15,75·10,25=161,43 кН                                                                                        V_тр=15,75·(49,5/2+10,25)=551,25Кн

Q_тр=551,25-161,43=389,82 кН

Прочность траверсы.

σ =М_пр/W_тр=4823,9·6/1,2·32²=21,5 кН/см²<R_yγ_c/γ_n=21·1/0,95=22,1 кН/см²

τ=389,82/1,2·32=10,15 кН/см²<0,58R_yγ_c/γ_n=0.58·21·1,0/0,95=12,82 кН/см²

Проверяем прочность траверсы как консольной балки

σ =М_е/W_тр=827,36·6/1,2·32²=4,03 кН/см²

Τ=Q_c/А_тр=161,43/1,2·32=4,20 кН/см²

σ _пр=√ σ ²+3²·τ=√4,03²+4,2²·3=8,32 кН/см²<1,15Rγ_c=1,15·22=25,3 кН/см²

Требуемая толщина швов, крепящих траверсу к полке ветви

К_ƒ=V_тр/2β_ƒℓ_еƒR_ωt=551,25/2·0,7(20,5-1)·18=0,7

Принимаем К_ƒ=0,8 мм

При расчете анкерных болтов растягивающее усилие наружной ветви в них вызывается комбинацией усилий с отрицательным изгибающим моментом. Расчетная комбинация при учете постоянной нагрузки и ветра слева

М´=+113,72·0,9/1,2+696,833=+782,123 кНм

N´=-121,43·0,9/1,2+61,35=-29,4 кН

При этом изгибающий момент и нормальная  сила от действия постоянной нагрузки принимаются с пониженным коэффициентом  надежности γ_n=0,9, а γ_t=1,2 – осредненный коэффициент надежности по нагрузке

Усиление в анкерных болтах

Ζ=-N_упр/в_о+М´/в_о=-29,4·0,52/1,1+782,123/1,1=697,13 кН

При учете постоянной ветровой и крановой (гр.13 сеч.4-4) нагрузки:

М´=-658,5 Кн

N=-189,31 кН.

М=-(658,5-113,72+113,72·0,9/1,2)=-630,07 кНм

N´=-(189,31-121,43)+121,43·0,9/1,2)=-158,95 кН

Ζ=-158,95·0,52/1,1+630,07/1,1=-75,14+572,7=+497,56 кН

Требуемая площадь нетто анкерных болтов

ΣА_вр=Ζ/R_ва=497,56/15=33,17, где

R_ва=15 кН/см² – расчетное сопротивление анкерных болтов из стали В_ст3нп2

Принимаем 2 болта d=56 мм с площадью 2·20,5=41 см² с общей несущей способностью N=2+403.5=807 кН

Усилие на один анкерный болт                                                        N_а=497·56/2=248,78

Изгибающий момент в анкерной плите                                                              М=248,78·30/4=1865,85 кН/см

Принимаем сечение анкерной плиты 240х70 мм с отверстиями для болта

D_а+8 мм=56+8=64 мм

Момент сопротивления нетто амперной плиты W_n=(25-6,4)·7²/6=151,9 см³

σ =M/W_n=1865.85/151.9=12,28 кН/см²=<_Ryγ_c/γ_n=20.5 кН/см²

3.6. Расчет подкрановой балки.

          Грузоподъемность крана Q=30/5 т; F_maxⁿ=380 кН, масса тележки