Разделение продуктов размола зерна в криволинейном потоке. Анализ сил действующих на частицу в циклоне разделителе (Отчет за второй год обучения в аспирантуре)

значительной мере зависит от размеров частицы и скорости их движения. Из-за сопротивления движения частицы поле течения в вихревом потоке в целом определяет траекторию частицы. Тем не менее, центробежные силы, действующие на частицу, противостоят увлечению их от перемещения к оси циклона. Центробежная сила есть следствие инерции, связанной с массой движущейся частицы, стремящейся перемещаться по прямой линии. Эту центробежную силу F_ц по А. Гупта, Д Лили, И. Сайр можно представить в виде

F_ц = C₁d³(ρ_ч – ρ_ср) ω²/r,                                         1.5

где  C₁ – постоянная,

        ρ_ч и ρ_ср – плотности частицы и среды соответственно,

        ω – окружная скорость,

        r – радиус.

Из уравнения 1.1 следует, что большие  F_ц возникающие в случае больших и плотных частиц, находящихся на малых радиусах, а также в случае малой плотности среды и высокой окружной скорости. Сила сопротивления F_с приближенно определяется выражением

F_с = C₂ d μ υ,                                                       1.6

где  C₂ – постоянная,

        μ – вязкость среды,

       υ – радиальная скорость среды.

Анализируя формулы 1.5 и 1.6 можно прийти к выводу, что на эффективность инерционной сепарации положительно влияют уменьшение размера частиц и использование среды с малой вязкостью.

В общем случае движение частицы в прямолинейном потоке создают в среде гидродинамические течения, определяющие сопротивление среды. В аэродинамике это сопротивление выражается формулой.

F_с = 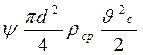                                                1.7

где     υ_с –  скорость относительного движения частицы,

           ψ – коэффициент сопротивления, являющейся однозначной функцией числа Рейнольдса.

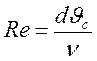
где     ν –  кинематическая вязкость среды.

Для малых скоростей движения и размеров частиц, тогда 0 < Re < 1, коэффициент сопротивления ψ может быть равен ψ = 24/ Re и формула 1.3 примет вид формулы Стокса

F_с = 3πμυ_с d                                                           1.8

Таким образом, Пирумов делает вывод, что в зависимости от размером частиц сопротивление их движению в одной и той же аэродинамической системе определяется различными законами. Лобовое сопротивление тел способно меняться в значительных переделах при изменении степени турбулентности оптикающего потока.

 Для упрощения аналитического решения задачи инерционной сепарации обычно пренебрегают также электростатическими силами, обусловленными заряженностью частиц.

В связи со сложностью учета ряда факторов при теоретическом анализе инерционной сепарации в криволинейном потоке необходимо ввести упрощающие допущения.

 Форма, размеры и строение поверхности частиц получается  случайно при размоле зерна в вальцевом станке и поэтому весьма разнообразны.

Любая фракция размола состоит из частиц различной формы. Поэтому обычно размеры частиц характеризуют какой-либо усредненной величиной, в качестве которой принимают ситовой (геометрический) размер, эквивалентный и гидравлический (семидентационный) диаметры.

При ситовом анализе размер частицы определяется размером ячейки минимального номера сита, через которое она еще может пройти. Однако, т.к. через одно и тоже отверстие могут проходить частицы различной формы (пластинчатые, сферические, продолговатые и д.т.) и массы, то очевидно, что ситовой размер d определяет движение частицы неоднозначно. Эквивалентный диаметр   d_эпредставляет собой диаметр шара, объем которого равен объему частицы. Для нахождения d_э  необходимо определить объем или массу частицы. Гидравлический диаметр d_Г равен диаметру сферической частицы с той же плотностью и скоростью витания υ_в, что и данная.

Относительная скорость частиц, размеры которых соизмеримы с размерами молекул, мало отличаются от нуля, в то время как крупные частицы могут приобретать скорость, доходящую до десятков метров