Модуль кусочно-линейного регрессионного анализа

Модуль кусочно-линейного регрессионного анализа.

Программа REFIER осуществляет построение кусочно-линейной регрессионной модели методом «фиксированных элементов разбиений» (5). Кусочно-линейная модель имеет вид

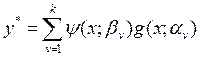, где к – количество областей разбиения {} всего пространства значений аргументов Х;

- параметрическая характеристическая функция области ;

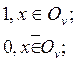
g(x, )- частная линейная регрессионная модель области ;

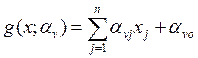
Каждая  строится методом наименьших квадратов на основе соответствующей подвыборки  объемом  реализации так, чтобы минимизировать величину

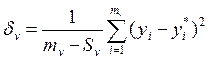, где

- число включенных в g(x, ) информативных факторов {}

Метод ФИЭР осуществляет отделение областей {} друг от друга гиперплоскостями, перпендикулярными тем или иным координатным осям {}. Поиск возможной границы области по каждому  осуществляется на основе границ  интервалов на его эмпирической шкале. Число интервалов разбиения  шкалы для каждого  задается. При =0 граница области по  не может быть реализована.

Метод предполагает предварительное построение некоторого количества (KMOD) различных локально-определенных линейных моделей. Обычно . Каждая такая модель строится на основе компактного множества KMOD исходных реализаций, «центральная» точка которого выбирается случайно из NО исходных. Обычно .

Количество к областей разбиения ограничивается заданной величиной . При этом, должно выполняться условие

Величина NOMIN также задается.

Качественные признаки  предварительно получают квази-количественное представление – каждое исходное значение  заменяется на среднее значение y для реализаций, у которых . В дальнейшем такие признаки анализируются как количественные.

Частные линейные модели строятся программой RGRF

Признаки, для которых , обязательно включаются в модель, а для которых - не включаются. Отбор информативных признаков среди тех, для которых задано, осуществляется поэтапно. Сначала рассматривается регрессионные модели от каждого из признаков  и от каждой пары исходных признаков выбирается наилучшая модель. Далее на каждом шаге в модель включается очередной информативный  - тот, включение которого дает наибольшее уменьшение величины . Построение модели осуществляется до тех пор, пока величина  уменьшается на каждом шаге в заданное (ZNACH) количество раз. Обычно . Число включенных признаков не более 30.

          Подпрограмма MKVK при построении той или иной частной модели на основе соответствующей ковариационной подматрицы решает систему линейных алгебраических уравнений методом квадратных корней по схеме Холецкого с двойной точностью. При плохой обусловленности системы находится ее регуляризованное решение с автоматическим выбором наилучшего значения параметра регуляризации.

          При построении кусочно-линейной модели минимизируется общий критерий

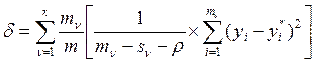,   (2.3)

где

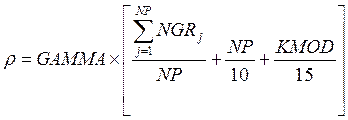
          Величину GAMMA целесообразно задавать в пределах . Чем меньше GAMMA, тем больше вероятность найти наилучшее разбиение  среди всех возможных, но тем и больше время решения задач.

          Границы каждой области  перпендикулярны некоторым автоматически выбранных исходным признакам . Например, для области О₁:

При этом области  будут принадлежать реализации, координаты

которых удовлетворяют всем указанным соотношениям. Рациональное количество областей к выбирается автоматически при минимизации . При этом величины  должны удовлетворять ограничениям  и .