


Алгоритм расчёта
Общей задачей линейного программирования (ОЗЛП) называется задача, состоящая в определении оптимального (максимального или минимального) значения линейной функции
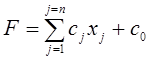 (l)
(l)
при условиях
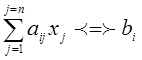 (i=1, 2, …, m) (2)
(i=1, 2, …, m) (2)
![]()
![]() (3)
(3)
где aij, ci, bi –
фиксированные действительные числа; ![]() – один из знаков отношения:
– один из знаков отношения: ![]() ,
, ![]() , = .
, = .
Другими словами,
в ОЗЛП ищется оптимальное значение
линейной функции (1) на множестве решений системы равенств и
неравенств (2) при условии неотрицательности некоторых переменных.
Заметим, что требование неотрицательности (3) может быть наложено на все
переменные (L = {1, 2, …, n}) или вообще
отсутствовать (L = 0).
Функция F называется линейной формой или целевой функцией задачи (1) – (3), а условия – (2) – (3) – ограничениями.
Совокупность чисел X=(x1, x2, ..., xn), удовлетворяющая ограничениям (2) – (3), называется допустимым решением или планом задачи.
План ![]() , при котором целевая функция принимает
минимальное или максимальное значение, называется оптимальным.
, при котором целевая функция принимает
минимальное или максимальное значение, называется оптимальным.
Таким образом, при любом плане X оптимальный
план X* удовлетворяет условию F(X*)![]() F(X)
(или F(X*)
F(X)
(или F(X*)![]() F(X)).
F(X)).
Не всякая задача линейного программирования имеет оптимальный план. Это связано с тем, что множество решений D системы ограничений (2) – (3) может быть пустым или форма F на D не ограничена снизу (сверху).
Множество D допустимых планов задачи (1) – (3) называют многогранником решений ОЗЛП. Может оказаться, что D = 0. D представляет собой некоторое подмножество конечномерного Евклидова пространства Rn. Особую роль в многограннике D играют его вершины, т. е. такие точки, которые не могут быть внутренними для любого отрезка, соединяющего две точки D. Обозначим множество вершин D через D0. Элементы D0 называются опорными планами ОЗЛП. Заметим, что D0 всегда конечно. Известно, что если D0 ≠ 0 и оптимум F существует, то он достигается хотя бы в одной из вершин D0. В связи с этим утверждением напрашивается такой способ решения ОЗЛП: найти множество D0 опорных планов и простым перебором определить требуемый оптимум F на D0. Пусть он равен F0 и F(X0) = F0 (X0ÎD0). Если при этом удается установить существование искомого оптимума F на D, то ясно, что он равен F0 и X0 – соответствующий оптимальный план задачи (1) – (3). Однако практически воспользоваться предложенным способом решения задачи линейного программирования затруднительно. Дело в том, что даже при относительно не большом числе ограничений и неизвестных получается астрономическое количество вершин. Да и сам процесс отыскания вершин не является простой процедурой.
Симплекс-метод решения канонических задач линейного программирования называют также методом последовательного улучшения плана. А название это объясняется тем, что в отличие от простого перебора вершин и вычисления значений формы F в них в симплекс-методе сначала определяют одну из вершин D, в которых значение F ближе к оптимуму.
Список использованных источников
1. Информатика: Учеб. пособие для пед. спец. высш. учеб. заведений / А.Р. Есаян, В.И. Ефимов, Л.П. Лапицкая и др. – М.: Просвещение, 1991. 288 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.