Определение нагрузок и воздействий на двускатную балку длиной 18 метров. Расчет железобетонной решетчатой балки

2.1.  Определение нагрузок и воздействий

              Нагрузка принята в соответствии со СНиП  2.01.07. - 85 Нагрузки и воздействия [3]

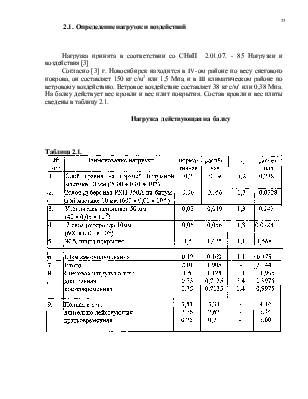
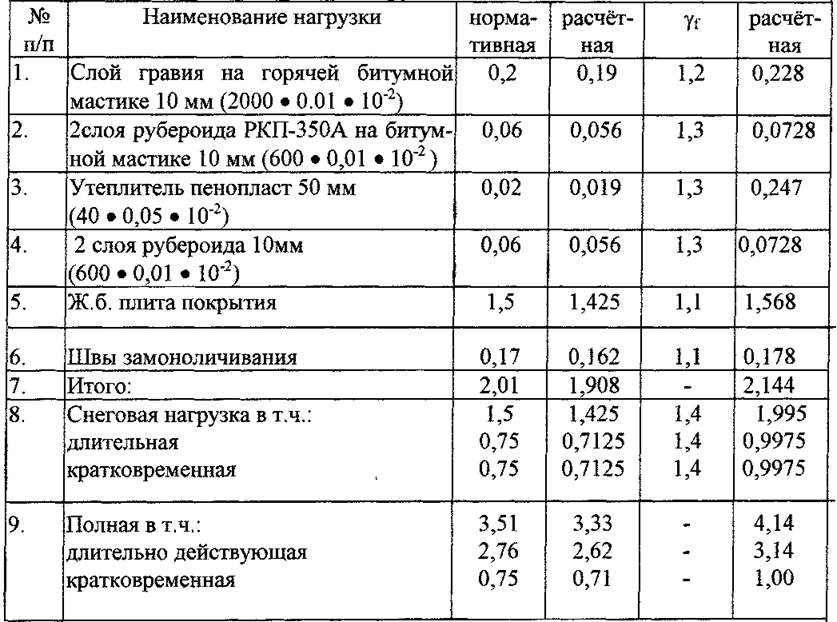
         Согласно [3] г. Новосибирск находится в IV-ом районе по весу снегового покрова, он составляет 150 кг с/м² или 1,5 Мпа, и в III климатическом районе по ветровому воздействию. Ветровое воздействие составляет 38 кг с/м' или 0,38 Мпа. На балку действует вес кровли и вес плит покрытия. Состав кровли и вес плиты сведены в таблицу 2.1.

Нагрузка  действующая на  балку

Таблица 2.1.

            2.2 Расчет железобетонной решетчатой балки

          2.2.1 Исходные данные

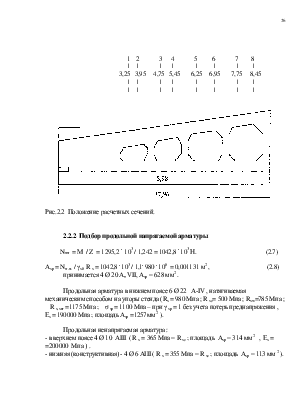
          Предварительно напряженная двускатная балка длиной 18 м. Расчетный пролет-

-17,7.  Уклон балки 1:12.

          Бетон тяжелый класса В40  ( R _b = 22 Mпа ;     R _{b, ser} = 29 Mпа ;      R _{b t}  = 1,4 Mпа ;

R _{b t , ser} = 2,1 Mпа;     Е _b = 32500 Mпа;)

          Балка нагружена сосредоточенными силами в узлах верхнего пояса, и распределенной нагрузкой от собственного веса.

          Нагрузка  на  1  м  балки  при  собственной  массе  10,4  т .   И  коэффициенте надежности по назначению   γ _n  = 0,95 и нагрузке  γ _f = 1.

                            g _nl 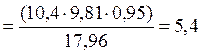  кН/м.                                                       (2.1)

Нагрузка при коэффициенте γ _f = 1,1

                            g _l  = 5,4 ^. 1,1= 5,94  кН/м.                                                                   (2.2)

            Расчетная схема решетчатой балки представляет собой свободно опёртую

многократно статически неопределимую замкнутую раму с жёсткими узлами. Для упрощения расчета в дипломном проектировании можно рассматривать решётчатую балку как балку с отверстиями.

                                                  Расчетная схема балки

                                2,85      3,00      3,00      3,00      3,00      2,85

                                                 Рис.2.1

            Значение сосредоточенной нагрузки

Расчетная нагрузка  4,14 ^. 3 ^. 6 = 74,52 кН .

Полная нормативная  3,51^. 3 ^. 6 = 63,18 кН .

Длительно действующая 3,14 ^.  3 ^. 6 = 56,62 кН .

            Изгибающие моменты в сечениях балки (рис.2.2) определяются по формуле:

                             М  = Q_x –g _l x² / 2 -  (G + S)_i  ^. (x – a _i ) ,                                           (2. 3)

где  х – расстояние от опоры до рассматриваемого сечения ;

       a _i – расстояние от опоры до рассматриваемого сечения .

            Поперечная сила на опоре :

при γ _f = 1  от полной нагрузки :

Q_max = g_nl 1_o/ 2+5^. (G_n + S_n) / 2 = 5,4^. 17,7 / 2 + 5^. 63,18 / 2 = 229,59  кН ,                   (2.4)

где G_n  - полная расчетная нагрузка , G_n  = 59,94 кН;

       S_n  - кратковременная расчетная нагрузка ,    S_n  = 12,78 кН.

От длительно действующей нагрузки:

Q _l , _max = g _nl 1_o / 2 + 5 G_n  / 2 = 5,4 ^. 17,7 / 2 + 5 ^. 56,62 /2 = 197,64 кН,                       (2.5)

при  γ _f > 1   от полной нагрузки:

Q_max = g _l 1_o/ 2+5 ^. (G + S) / 2 = 5,94 ^. 17,7 / 2 + 5 ^. 74,52 /2 = 283,87  кН                    (2.6)

где G  - полная расчетная нагрузка;

       S  - кратковременная расчетная нагрузка.

            Значения моментов, кН  ^. м , сведены в таблицу 2.2

Таблица 2.2  Изгибающие моменты в расчетных сечениях , кН  ^. м

                                                      1    2             3      4             5          6             7         8