Основные формулы математической статистики

Стандартное отклонение – величина именованная, выраженная в тех же единицах измерения, как и средняя арифметическая.

Поэтому для сравнения разных признаков, выраженных в разных единицах измерения, используется не абсолютное, а относительное значение стандартного отклонения в форме коэффициента вариации:

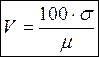, где

σ – стандартное отклонение;

μ – средняя арифметическая.

Асимметрия

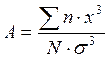
Правосторонняя асимметрия – отрицательна, левосторонняя–положительна.

Эксцесс

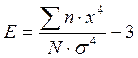
Эксцесс положителен при островершинной кривой, отрицателен при плосковершинной.

Ошибка репрезентативности (выборочной средней)

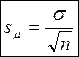
 – возможная максимальная абсолютная погрешность при прогнозе генерального параметра;

t – критерий надежности, или показатель вероятности того, что величина генерального параметра действительно будет находиться внутри найденных доверительных границ;

 – максимальная доверительная граница, или возможный максимум;

 – минимальная доверительная граница, или гарантированный минимум.

Три порога надежности (вероятности безошибочных прогнозов)

Показатель точности

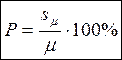
Ошибка стандартного отклонения

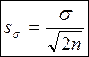
Ошибка коэффициента вариации

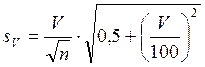
Ошибка показателя асимметрии

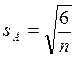
Ошибка показателя эксцесса

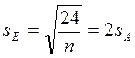
Средняя ошибка суммы нескольких средних

Средняя ошибка произведения двух выборочных средних

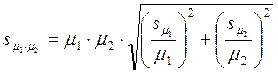
Средняя ошибка частного двух выборочных средних

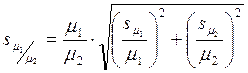
Средняя ошибка разности выборочных средних двух независимых распределений

При n₁ = n₂

При n₁≠n₂

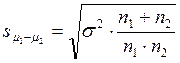
σ – объединенная дисперсия двух выборок

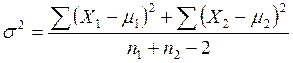
Средняя ошибка разности в парных опытах

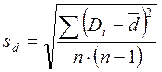
D_i – разности между вариантами сопряженных рядов X₁ и X₂;

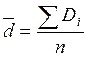
n – общее число парных наблюдений.

Корреляция. Коэффициент корреляции

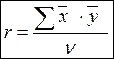, где

– нормированные отклонения данных по первому и второму признаку;

n= n–1 – число степеней свободы, равное в данном случае числу сравниваемых пар без одной.

          

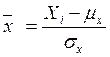
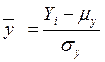
Ошибка репрезентативности коэффициента корреляции:

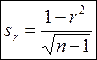
Коэффициент прямолинейной регрессии

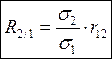, где

s₂ – стандартное отклонение второго признака, который изменяется в связи с изменением первого;

s₁ – стандартное отклонение первого признака, в связи с изменением которого изменяется второй признак;

r₁₂ – коэффициент корреляции между первым и вторым признаками.

Уравнение прямолинейной регрессии

(X₂-μ₂)=R_2/1 (X₁- μ ₁)

Ошибка коэффициента регрессии

.

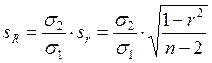Корреляционное отношение второго признака по первому

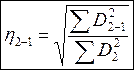, где ,

Примерное значение ошибки квадрата корреляционного отношения η²

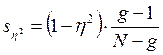, где

g – число классов первого признака;

N – объем выборки.

Критерий достоверности (F) и доверительные границы квадрата корреляционного отношения

,

,

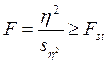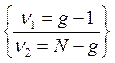
Критерий линейности корреляции

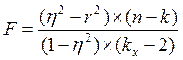, где

η² – квадрат корреляционного отношения Y по Х;

r² – квадрат коэффициента линейной корреляции;

n – объем выборки;

k_x – число групп по ряду X.

Связь можно практически принять за линейную, если F_факт < F_теор. Корреляция нелинейная, если F_факт ≥ F_теор.

Частные коэффициенты корреляции

;

;

.

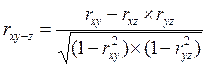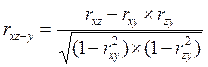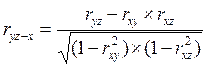Множественный коэффициент корреляции трех переменных – это показатель тесноты линейной связи между одним из признаков (буква индекса перед тире) и совокупностью двух других признаков (буквы индекса после тире):

;

;

.

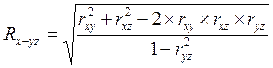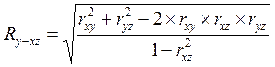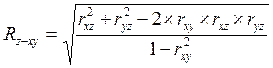Значимость множественной корреляции оценивается по F–критерию:

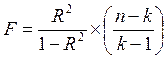, где:

n – объем выборки,

k – число признаков.

Множественное линейное уравнение плоскости регрессии

Однофакторный статистический комплекс

, где

С_Y – сумма квадратов по всему комплексу;

С_V – сумма квадратов между выборками;

C_z – сумма квадратов внутри выборок.

N – 1 – общее число степеней свободы;

l–1 – степени свободы для вариантов и N–l для случайного варьирования.

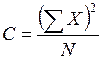 – корректирующий фактор (поправка);

 – общая сумма квадратов;

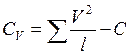 – сумма квадратов для вариантов;

 сумма квадратов для ошибки (остаток).

Оценка значимости действия изучаемых факторов

.

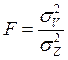Если F_факт < F_теop, то нулевая гипотеза Но: d = 0 не отвергается; между всеми выборочными средними нет существенных различий. Нулевая гипотеза отвергается, когда F_факт ≥ F_теop.

Многофакторный дисперсионный анализ

В двухфакторном опыте, поставленном методом обычных повторений, сумма квадратов для вариантов C_V расчленяется на три, а в трехфакторном – на семь компонентов. Общая сумма квадратов для этих опытов будет представлена следующими выражениями (в скобках указаны суммы квадратов