












Рассмотрим теплопроводность плоской многослойной стенки , состящей из nслоев , плотно прилегающих один к другому. Каждый слой имеет заданную толщину d и коэф- т теплопроводности l . Многослойными являются , например стены и перекрытия крупнопанельных и кирпичных зданий.
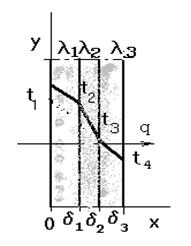
При стационарном тепловом режиме тепловой поток, проходящий через каждый из слоев стенки, не изменяется. Поэтому, пользуясь формулой ( 1.11) для каждого слоя можно написать :
q = l1 /d1( t1 - t2); q = l2 /d2( t2 - t3); q = l3 /d3 ( t3 – t4) ( 1.14)
разрешив уравнения относительно разности температур и просуммировав правые и левые части этих равенств, получим q , Вт /м2:
q = (t-t)/( d1 / l1 + d2 / l2 +d3 / l3 ) = Dt/ SR, ( 1.15 )
где :
Dt - температурный перепад , т.е. разность температур парных поверхностей стенки;
SR - общее термическое сопротивление многослойной стенки, равное сумме термических сопротивлений отдельных слоев.
Для построения температурного поля многослойной стенки необходимо знать температуру на поверхности каждого слоя в отдельности, которая определяется из следующих очевидных равенств:
q=t1-t2/(d1 / l1)= t2-t3/(d2 / l2)и т.д. ( 1.16)
Температурное поле многослойной стенки изобразится ломанной линией. Тепловой поток Q, Вт, через многослойную плоскую стенку определяется по формуле 2-13
Пусть имеется труба с внутренним диаметром d1 и внешним d2, соответственно r1 и r2 Труба состоит из материала с теплопроводностью l и имеет температуру внутренней стенки t1, температуру внешней-t2. Т.к. удельный поток q является переменным по толщине стенки, то следует рассматривать полный тепловой поток Q.
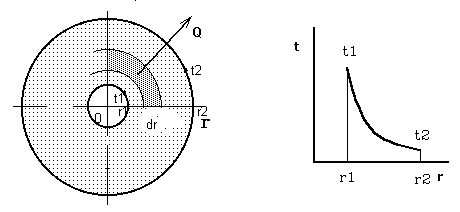
Выделим элементарный слой толщиной dr. Тогда, согласно 1.6 можно записать
Q=l (dt/dr)2prl1.17
Разделяя переменные и интегрируя, получим
t=(Q/2pl)lnr+C(1.18)
Откуда несложно получить тепловой поток, проходящий через 1 погонный метр боковой поверхности
Ql=2pl(t2-t1)/ln(d2/d1)(1.19)
Из формулы 1.18 видно, что температура в стенке трубы изменяется по логарифмическому закону. Это следует учитывать при толщине изоляции соизмеримой с диаметром трубы. Для тонких стенок можно пользоваться формулой 1.12.
Лекция 6. 1.3.Конвективный теплообмен
Тепловой поток Q ,Вт, передаваемый при конвективном теплообмене, определяется по формуле Ньютона-Рихмана:
Q=αK(tЖ-tC)F ( 1.20)
, где αK – коэффициент пропорциональности, называемый коэффициентом теплоотдачи;
tЖ – температура теплоносителя; tC – температура поверхности стенки; F – поверхность соприкосновения со стенкой .
Формулу ( 1.21) можно использовать, как и при теплоотдаче от жидкости или газа к стенке или наоборот.
Приняв F=1м2 , получим удельный тепловой поток q, Вт/м2:
q=α(tЖ-tC) ( 1.21)
1/a=R- термическое сопротивление теплоотдачи
Физическая модель конвективного теплообмена
Пусть унас имеется нагретая поверхность омываемая холодным потоком жидкости или газа. Тогда тепловой поток от поверхности будет направлен в сторону жидкости , и по мере движения, жидкость будет нагреваться. Возле стенки формируется гидродинамический пограничный слой, в котором происходит сдвиговое течение, т.е на стенке частицы прилипают wСТ=0. по мере удаления скорость увеличивается и за пограничным слоем остается постоянной w=w0. Под воздействием температурного напора формируется тепловой пограничный слой, в реальных жидкостях его толщина dТ соизмерима с гидродинамическим dГ. Для него характерно – температура на стенке равна tСТ, в пограничном слое параболически изменяется и за погранслоем остается постоянной t0. Вследствие сдвигового течения (слои не смешиваются) в погранслое, теплота поперек движения распространяется теплопрововодностью а в продольном направлении- переносится потоком (конвекцией).
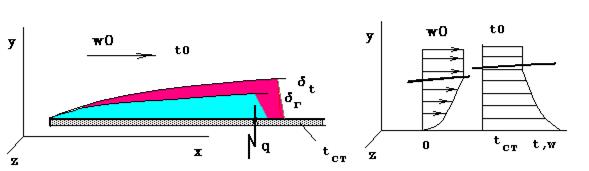
Наличие теплового погранслоя можно определить чувствительной термопарой или поднеся ладонь к раскаленной плоскости (утюга) почувствовать резкое увеличение температуры-его толщина составляет 2-3мм.
По мере продвижения жидкости вдоль поверхности его толщина увеличивается до тех пор, пока не наступит переходный, а затем турбулентный режим. Произойдет разрушение (утоньшение) погранслоя. Локальный коэффициент теплоотдачи как и тепловой поток будет изменяться обратно пропорционально его толщине, что следует из закона Фурье q~1/dт .
|
|
Обтекание потоком нагретого цилиндра. Темные полосы соответствуют изотермам в потоке. Видно наростание погранслоя и отрыв нагретых слоев в корме. |
Рис.
В целом такой сложный процесс называется конвективной теплоотдачей
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.